Find the answer for this?
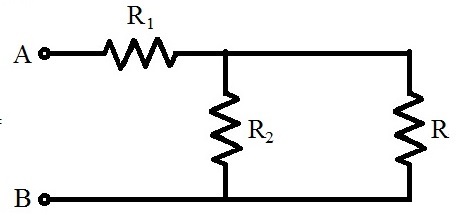
The circuit shown above has resistances and . With a constant voltage between and , at what value of resistance will the thermal power generated in it be practically independent of small variations of its resistance?
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the voltage between A and B be V A B and the voltage across R be V . Then the power generated by R is given by:
P = R V 2 = ( R 1 + R 2 ∣ ∣ R R 2 ∣ ∣ R V A B ) 2 × R 1 = ( 2 0 + 3 0 ∣ ∣ R 3 0 ∣ ∣ R ) 2 R V A B 2 = ( 2 0 + R + 3 0 3 0 R R + 3 0 3 0 R ) 2 R V A B 2 = ( 5 R + 6 0 ) 2 9 R V A B 2
Let us find the change of P due to a change in R .
d R d P = ( 5 R + 6 0 ) 3 2 9 ( 5 R + 6 0 ) − 2 ⋅ 9 R ( 5 ) = ( 5 R + 6 0 ) 3 5 4 0 − 4 5 R
⟹ d R d P = 0 , when 4 5 R = 5 4 0 ⟹ R = 1 2 Ω .