FIND THE ANSWER OF THIS QUESTION...............
Algebra
Level
3
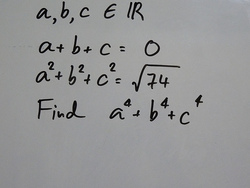 find the value of asked in respect......
find the value of asked in respect......
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It's really a nice problem. So we have 2 equations and 3 variables??? a + b + c = 0 a 2 + b 2 + c 2 = 7 4 We know that: ( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 ( a b + b c + a c ) 0 = 7 4 + 2 ( a b + b c + a c ) a b + b c + a c = − 2 7 4 Let us assume a equation with a , b , c as its roots so sum of roots is 0 and sum of product of roots taken two at a time is − 2 7 4 .
Hence the equation is x 3 − 2 7 4 x + k = 0 Here k is any constant. Putting a in the equation: a 3 = 2 7 4 a − k Similarly for b and c . The expression we have to find is a 4 + b 4 + c 4 = a 3 a + b 3 b + c 3 c = a 2 2 7 4 − a k + b 2 2 7 4 − b k + c 2 2 7 4 − c k = 2 7 4 ( a 2 + b 2 + c 2 ) − k ( a + b + c ) = 2 7 4 − 0 = 3 7