Find the area...
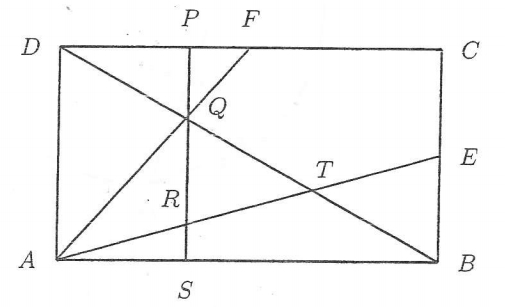
The diagram above shows a rectangle A B C D such that E is the midpoint of B C and F is the midpoint of C D . The diagonal B D intersects A F and A E at Q and T respectively. The vertical line P S passing through Q is perpendicular to A B and intersects A E at R . It is also given that A B = C D = 1 2 and B C = A D = 6 .
Find the area of the triangle △ Q R T .
This is a part of the Set .
The answer is 6.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Use coordinates geometry, with A(0,0).The equation of lines AF : y=x, BD:y=-0.5x+6,AE:y=0.25x, Then we will find the coordinates of intersection points Q(4,4),R(4,1), and T(8,2). The area of the triangle QRT = (1/2)(4)(3) = 6.
Easiest approach if you asked me!
△ E T B and △ A T D are similar trianlges. So, A T E T = D T B T = A D E B = 2 1
⟹ a = E T = 3 A E = 3 1 2 2 + 3 2 = 1 7 ,
b = B T = 3 B D = 3 1 2 2 + 6 2 = 2 5
and c = E B = 3
△ E T B = s ( s − a ) ( s − b ) ( s − c ) [ where s = 2 a + b + c ] = 4 1 2 a 2 b 2 + 2 b 2 c 2 + 2 c 2 a 2 − a 4 − b 4 − c 4 = 4 1 5 7 6 = 6
Now, △ A Q B and △ F Q D are also similar triangles.
⟹ B Q D Q = A B D F = 2 1 ⟹ T Q = B T = D Q = 3 B D
But P S and C B are parallel straight lines. So, ∠ T Q R = ∠ T B E and ∠ T R Q = ∠ T E B .
Then, △ E T B ≅ △ Q R T ⟹ △ Q R T = 6
The area of the rectangle is 6*12=72. Areas of triangles FDA and EAB each is 4 7 2 . So the area of F A E C F = 7 2 − 4 7 2 − 4 7 2 = 2 7 2 = 3 6 . S o a r e a o f △ F A E = a r e a o f F A E C F − a r e a o f △ C F E . = 3 6 − 2 1 ∗ 3 ∗ 6 = 2 7 . Property of a rectangle Q and T trisects the diagonal DB. ∴ Q T = 3 1 ∗ D B . ∴ i n △ C D B , F E = 2 1 ∗ D B . ∴ F E Q T = 3 2 . I n △ T D A , Q i s m i d p o i n t , Q R ∣ ∣ D A . ∴ R i s m i d p o i n t o f A T . A r e a s △ Q R T = 2 1 ∗ △ Q A T = 2 1 ∗ ( F E Q T ) 2 ∗ △ F A E = 2 1 ∗ ( 3 2 ) 2 ∗ 2 7 = 6 P r o o f o f T r i s e c t i o n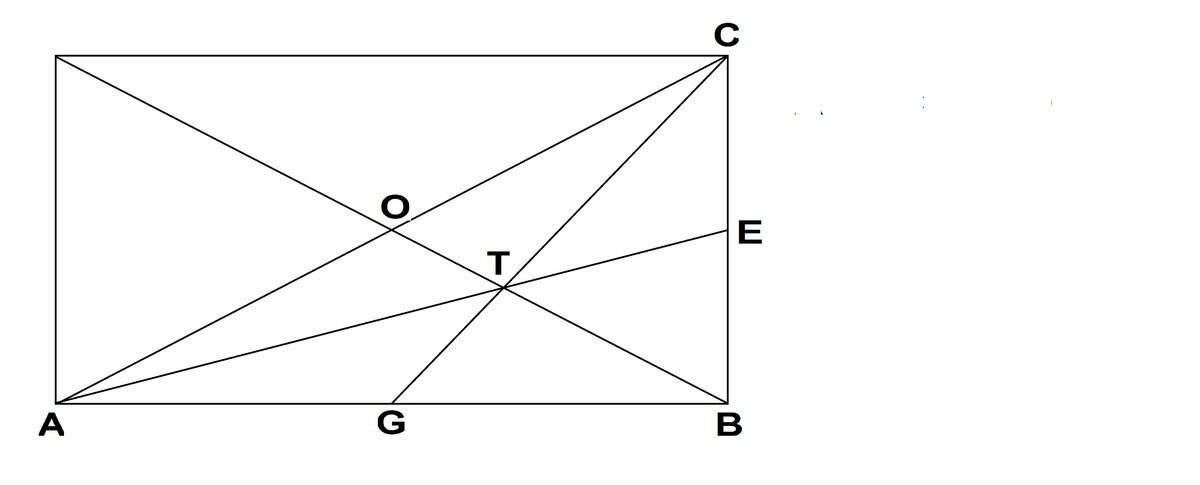 Draw the other diagonal CA to bisect diagonal DB at at O.
Let G be the midpoint of AB. Draw GC
⟹
i
n
△
C
A
B
,
B
O
,
C
G
,
A
E
,
a
r
e
m
e
d
i
a
n
s
c
o
−
i
n
c
i
d
e
n
t
a
t
T
.
S
o
B
T
=
3
2
∗
B
O
=
3
1
∗
B
D
.
⟹
T
t
r
i
s
e
c
t
s
t
h
e
d
i
a
g
o
n
a
l
.
Draw the other diagonal CA to bisect diagonal DB at at O.
Let G be the midpoint of AB. Draw GC
⟹
i
n
△
C
A
B
,
B
O
,
C
G
,
A
E
,
a
r
e
m
e
d
i
a
n
s
c
o
−
i
n
c
i
d
e
n
t
a
t
T
.
S
o
B
T
=
3
2
∗
B
O
=
3
1
∗
B
D
.
⟹
T
t
r
i
s
e
c
t
s
t
h
e
d
i
a
g
o
n
a
l
.