Find the area
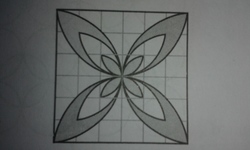 The given figure is created by using the arcs of quadrants with radii 1cm, 2cm and 3cm. Find the total area of the shaded region. (Take
π
=
3
.
1
4
)
The given figure is created by using the arcs of quadrants with radii 1cm, 2cm and 3cm. Find the total area of the shaded region. (Take
π
=
3
.
1
4
)
The answer is 13.68.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Looking at the case of one quadrant and one arc :
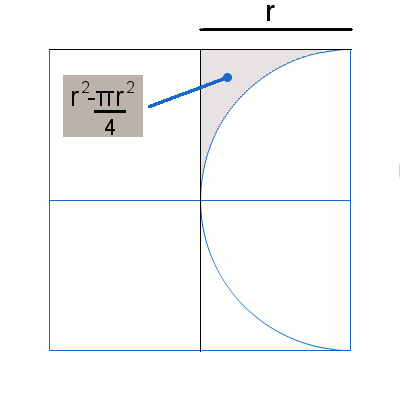
The shaded area is r 2 − 4 π r 2
Therefore when both arcs are present the total area of one petal : p(r) {the area in one quadrant bounded by the two arcs of radius r) :
p ( r ) = r 2 − 2 ( r 2 − 4 π r 2 ) = r 2 − ( 2 r 2 − 2 π r 2 ) = r 2 − r 2 ( 2 − 2 π ) = r 2 ( 1 − ( 2 − 2 π ) ) = r 2 ( 2 π − 1 )
Looking now at the full problem - the shaded area there is :
4 ( p ( 3 ) − p ( 2 ) + p 1 ) = 4 ( 9 ( 2 π − 1 ) − 2 ( 2 π − 1 ) + ( 2 π − 1 ) ) = 4 ( ( 2 π − 1 ) ( 9 − 4 + 1 ) = 4 ∗ 6 ∗ ( ( 2 π − 1 ) = 1 2 π − 2 4 = 1 3 . 6 8
The precise area is 13.69911184307
Moderator note:
Why? How did you arrive at that conclusion?
consider half of the figure. Area of semicircle is πr2/2 subtract the right Δ from that the sides of that are 2r, r√2 & r√2. Area is r2. So one petal area is r2 ( π/2 – 1). Total area of 4 petals 4*(r12 – r22 + r32 ) (π/2 – 1) = 4(9 – 4 + 1)(π/2 -1) = 13.7 cm2
Taking only the portion between vertical central line and line from the center at 45 degrees to the first line. One eighth of the whole.
The area covered by an arc= Quarter circle - half sqare. = 4 1 ∗ π ∗ r 2 − 2 1 ∗ r 2 . O u t e r a r c : − A r e a = 4 1 ∗ π ∗ 3 2 − 2 1 ∗ 3 2 . . . . . . . . . . . . . . . . . . . . . . . ( 1 ) M i d d l e a r c : − A r e a = 4 1 ∗ π ∗ 2 2 − 2 1 ∗ 2 2 . . . . . . . . . . . . . . . . . . . . . . . ( 2 ) I n n e r a r c : − A r e a = 4 1 ∗ π ∗ 1 2 − 2 1 ∗ 1 2 . . . . . . . . . . . . . . . . . . . . . . . ( 3 ) S h a d e d A r e a = ( 1 ) − ( 2 ) + ( 3 ) = 4 1 ∗ π ∗ 6 − 3 So for the whole shaded area = 8 ∗ { 4 1 ∗ π ∗ 6 − 3 } 1 3 . 6 8