Find The Area
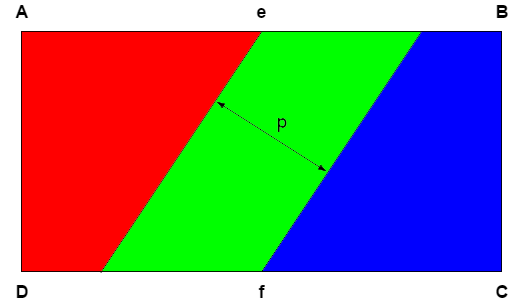
The rectangle A B C D is twice as wide as it is high. Parallel lines which are a distance of p apart cross the mid-point of the long sides of the rectangle at e and f as shown. All 3 regions (red, green, blue) are of equal area.
What is the area of the rectangle A B C D as a function of p ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Call the width of the rectangle 2L and the height L (we are told that the width is twice the height). The overall area of the rectangle will therefore be 2 L 2 .
Calculate the area of one of the trapezoids (the red or blue areas) which has one side and a base of length L. Call the other side y. This trapezoid's area will be 1/3 of the overall area. ( 3 2 L 2 ).
Therefore we have 3 2 L 2 = L 2 ( L + y ) which gives y = 3 L .
Now look at the parallel lines. If you split the rectangle into 2 squares, the area between the parallel lines forms a right-angled triangle and will be 1/6 of the area of the rectangle. We don't know the length of the hypotenuse but we do know the other two sides. One is L and the other is L-y (which is 3 2 L ).
Using Pythagoras, we can calculate the hypotenuse to be 3 1 3 L .
The area of this triangle will be 2 b a s e ∗ h e i g h t which will be equal to 6 2 L 2 . The height of this triangle is p. Therefore we have... 6 1 3 L p = 6 2 L 2 .
Solving this give us L = 2 1 3 p .
And we know the area of the rectangle is 2 L 2 . This then gives us...
A = 2 ( 2 1 3 p ) 2 = 2 1 3 p 2 .
Holy crap. This took me a while
pls hw is the area of the trapezium 1/3 the total area?
Log in to reply
Notice that
All 3 regions (red, green, blue) are of equal area.
Log in to reply
oh thanks. pls sir can u make the points to a question visible on phones just like before?
Is not hard to see that the side of the parallelogram is a third of the longer side. Half of this parallelogram is a rectangle triangle of sides proportional to 2 , 3 , 1 3 Let p = 3 x The base of the parallelogram is then 1 3 x Then the area of the rectangle is ( 3 1 3 x ) ( 3 / 2 1 3 ) = 2 9 x 2 1 3 = 2 1 3 p 2 :)
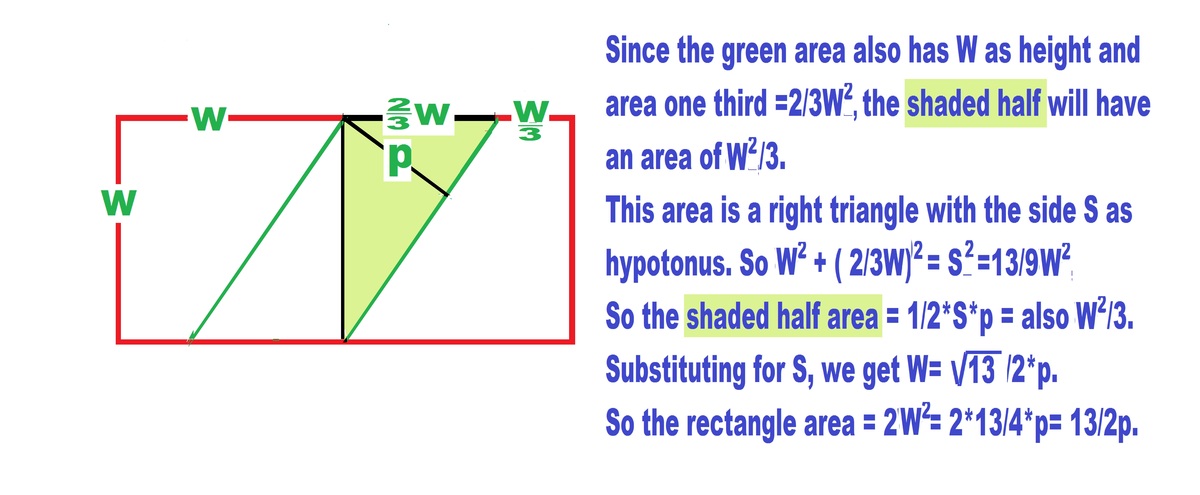
The dimensions of the rectangle are 2 a × a ; we must calculate 2 a 2 .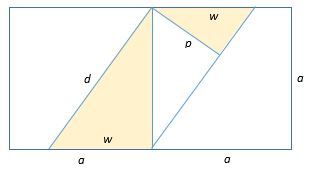
Let w be the width of the green parallelogram. Then w = 3 2 a to make the three areas equal. The slanted sides of the parallelogram have length d = w 2 + a 2 = ( 3 2 a ) 2 + a 2 = 3 1 1 3 a . Using similar triangles, d a = w p , so that 3 2 a 2 = p d = 3 1 1 3 p a . Thus we find a = 2 1 1 3 p and the area of the rectangle is 2 a 2 = 2 1 3 p 2 .