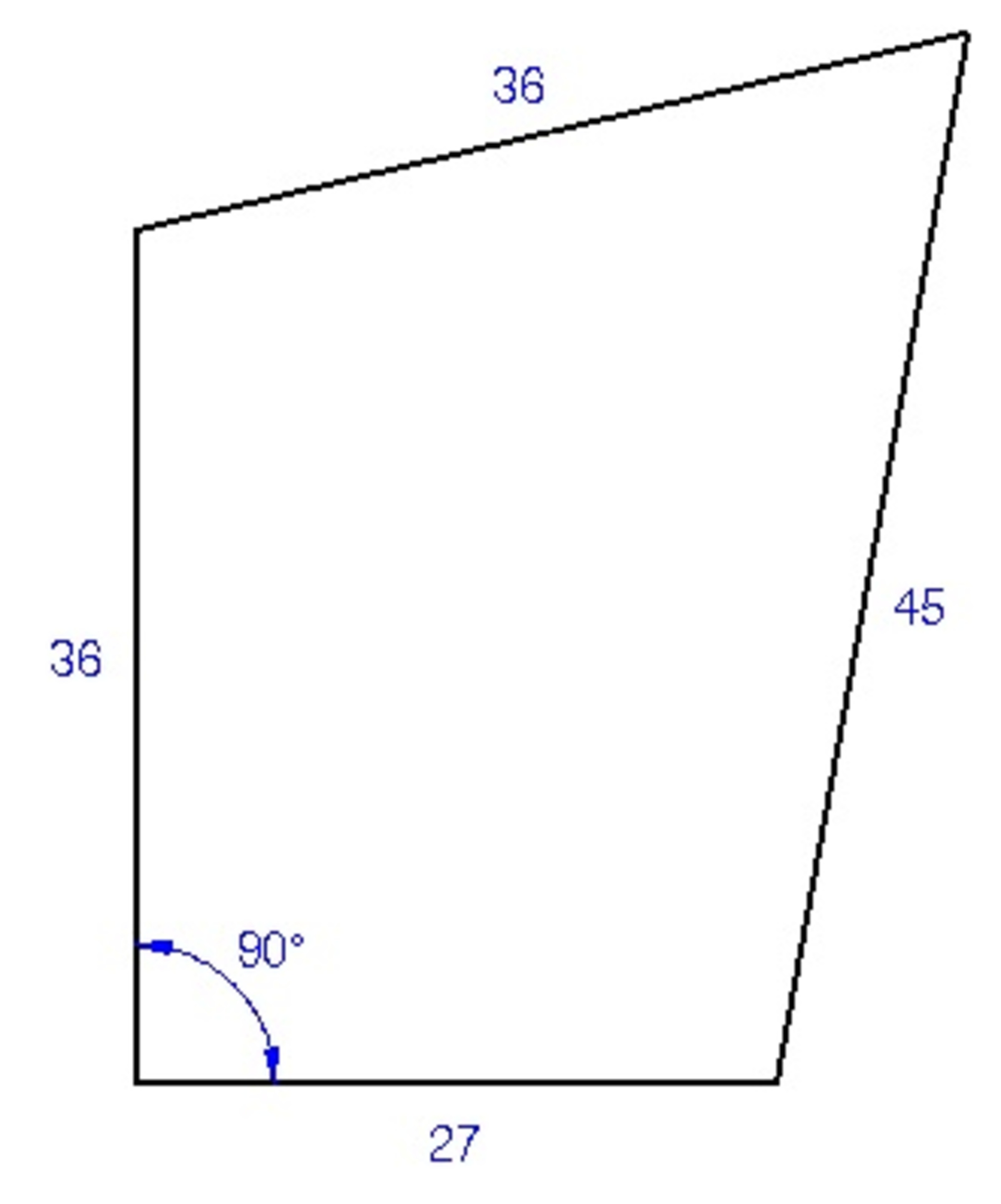
Find the area
Find the area of the figure shown below.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
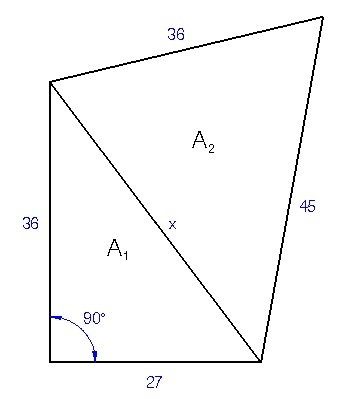 Apply
pythagorean theorem
Apply
pythagorean theorem
x 2 = 3 6 2 + 2 7 2 ⟹ x 2 = 1 2 9 6 + 7 2 9 ⟹ x 2 = 2 0 2 5 ⟹ x = 2 0 2 5 ⟹ x = 4 5
Compute A 1 :
A 1 = 2 1 b h = 2 1 ( 3 6 ) ( 2 7 ) = 4 8 6
Compute A 2 using the Heron's Formula :
s = 2 3 6 + 4 5 + 4 5 = 6 3 ⟹ A 2 = s ( s − a ) ( s − b ) ( s − c ) = 6 3 ( 6 3 − 3 6 ) ( 6 3 − 4 5 ) ( 6 3 − 4 5 ) = 6 3 ( 2 7 ) ( 1 8 ) ( 1 8 ) = 1 6 2 2 1
Finally, A = A 1 + A 2 = 4 8 6 + 1 6 2 2 1 answer
162 x sqrt(21) = sqrt(172 x 162 x 21) = sqrt (551124). So it seems that the 3rd answer is correct too.
Log in to reply
unless it has been edited, the third one actually has an extra 1 in the middle of the number (5511124) so it's not actually correct but it only looks correct. The same can be said for the fourth option because another way of expressing the correct answer would be the option 4 but with sqrt(1701) so it seems like all the incorrect options might have been written in a way to trick people into clicking on them by looking almost exactly like a correct answer.
Pythagorean theorem in the green one gives us the length of the diagonal of the quadrilateral as 3 6 2 + 2 7 2 = 4 5
The yellow triangle is isosceles and its height, marked with a dashed line, is from Pythagorean theorem 4 5 2 − 1 8 2 = 9 2 1
Area of green triangle A g = 2 1 × 3 6 × 2 7 = 4 8 6
Area of yellow triangle A y = 2 1 × 3 6 × 9 × 2 1 = 1 6 2 2 1
Total area A = A g + A y = 4 8 6 + 1 6 2 2 1