Find the area

Geometry Level 5

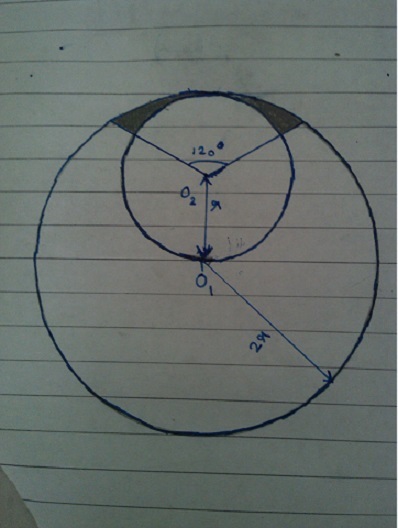A circle with centre ${ O }_{ 1 }$ and radius $2r$ is drawn. A point ${ O }_{ 2 }$ is taken at a distance $r$ from ${ O }_{ 1 }$ . Now a circle is drawn with centre ${ O }_{ 2 }$ and radius $r$ . Now two lines are drawn from ${ O }_{ 2 }$ each making an angle ${ 60 }^{ 0 }$ with ${ O }_{ 1 }$ ${ O }_{ 2 }$ produced and the given figure is obtained.

If the area of the shaded region in the given figure can be written as $A=k{r}^{2}$ then find $\left\lfloor 100k \right\rfloor$ .

Note: The starting part of the question is just a description of how the figure is drawn. The figure must be taken as the reference for finding the shaded region.

Also try Let's play pool .

The answer is 22.

3 solutions

Chew-Seong Cheong
Jul 6, 2014

Let the $2r$ -arc of the shaded area to end at points $P$ and $Q$ . The required area $A = A_{1}$ area of the sector $O_{1}PQ - A_{2}$ area of $\frac{1}{3}$ of the smaller circle $-A_{3}$ area of the two similar triangles $\triangle O_{1}O_{2}P$ and $\triangle O_{1}O_{2}Q$ .

To find $A_{1}$ and $A_{3}$ we need to know $\angle PO_{1}O_{2} = \angle QO_{1}O_{2} = \theta$ . Let the line $PQ$ meet the extension of $O_{1}O_{2}$ at $R$ . Let $O_{2}R$ , $PR$ and $O_{2}P$ be $a$ , $b$ and $c$ respectively.

Since $\angle PO_{1}O_{2}=60^{\circ}$ , $b=\sqrt{3}a$ and $c=2a$ . We know that $O_{1}R^{2}+PR^{2}=O_{1}P^{2}$ .

$\begin{aligned} \implies (r+a)^{2}+b^{2}& =(2r)^{2} \\ (r+a)^{2}+(\sqrt{3}a)^{2} & =(2r)^{2} \\ r^{2}+2ar+a^{2}+3a^{2}& =4r^{2}\\ 4a^{2}+2ra-3r^{2} & =0 \end{aligned}$

Solving the quadratic equation for $a$ , we have $a=\dfrac{\sqrt{13}-1}{4}r$ . Then $\cos\theta=\dfrac{a+r}{2r}=0.825693909$ , and $\theta=cos^{-1}0.825693909= 0.599365154$ rad. Now,

$A=A_{1}-A_{2}-A_{3} = kr^{2}$

$A_{1}=\frac{2\theta}{2}(2r)^{2}=4\theta r^{2}=2.397460617r^{2}$

$A_{2}=\frac{1}{3}\pi r^{2}=1.047197551r^{2}$

$A_{3}=2r(\frac{1}{2}b)=\sqrt{3}ar=1.128236798r^{2}$

$\Rightarrow A = (2.397460617 - 1.047197551 - 1.128236798)r^{2} = 0.222026268 r^{2}$

$\Rightarrow k=0.222026268$

$\Rightarrow \left\lfloor 100k \right\rfloor = \boxed{22}$

You can use double integral in polar coordinates to find the shaded area

Nguyễn Quang - 6 years, 10 months ago

There's a typo - $\angle PO_1O_2\neq 60^{\circ}$ ... You had in mind a different angle. great proof otherwise.

mathh mathh - 6 years, 10 months ago

Very complex solution

Kïñshük Sïñgh - 6 years, 11 months ago

Actually this question was intended to have a complex solution. There is no easier way to do this

Ronak Agarwal - 6 years, 11 months ago

i think mine is easier !

A Former Brilliant Member - 4 years, 5 months ago

Yes, this is nonlinear curve (quadratic curve), and does not have direct relationship with either smaller or larger circle. Both the circle share some information related to the shaded region. It is part of the larger circle (2r) and resulted as an extension of the radius of smaller circle (r) with 120-degree angle at the center (O2). So, it is not direct, it has to be complex. Thanks for the solution!

Parmod Kumar - 6 years, 10 months ago

I came up with this solution but the one with obtuse triangle is much easier. Area of sector of bigger circle subtracted by the sum of sector of the other circle and twice the area of the triangle.

Kim Chan - 6 years, 10 months ago

I didn't get it how the angle PO1O2 = 60? I should be 30.

Srabon Megh - 6 years, 10 months ago

A should be easily equal to: \frac{1}{6} \times S {O1} - \frac{1}{3} \times S {O2} - \frac{2}{3} \times S_{O1PQ}

Linkin Duck - 6 years, 10 months ago

could have assumed equations for circles and lines and then integrated to find area

Akshay Bodhare - 6 years, 10 months ago

In my solution I used Trigonometry:

Area(shaded) = AS1(O1,2r,2b)) - AS2(O2,r,2a) - 2At(O1O2P);

AS2(O2,r,2a0) = (a0)r^2 = (1/3)Pi*r^2,

a0 = (1/3)Pi half angle of the sector S2;

Let (R;A) a sistem of a polar coordinates on the plane with center O2,

axis y, so:

x = 0, is for O1O2, (segment of axis y)

so y = 0, is perpendicular to axis y with positive values to right side;

Let P, Q; P1, Q1 the intersection points between left and right rays

from O1, and Circle(O1,2r) and Circle(O2,r) rispectively;

L, L1 the intersection between perpendicular to x axis from Q, Q1,

and M the intersection between O2P an perpendicular to O2P and

O2P; c = angle(Q1O1Q); d = angle(O1QO2)

we have: Pi/2 - A = 2(Pi/2 - (B + c)), so:

B = (Pi/2 + A - 2c)/2, and

d = B - A, so: d = (Pi/2 - A -2c)/2;

R^2 = x^2 + y^2;

Translating from O2 in O1 we have a sistem of polar coordinates

(R',B), with axis X,Y so that for Circle(O1,2r):

X = (2r)cosB = x;

Y = (2r)sinB;

X = x;

Y = y + r;

Equation of Circle(O2,r):

x^2 + y^2 = r^2; => R = r;

Equation of Circle(O1,2r): .

x^2 + (y + r)^2 = 4r^2;

x^2 + y^2 + 2ry + r^2 = 4r^2 x = (2r)cosB;

y + r = (2r)sinB;

y = r(2sinB -1);

x^2 + y^2 = 3r^2 -2ry =>

R^2 = (r^2)(5 - 4sinB);

R = r√(5 - 4sinB)

now we have for the sines theorem applied to triangle(O1O2P):

O1P/sin(Pi/2 + A) = O1O2/sin(d), =>

2r/cosA = r/√((1-sin(A + 2c))/2);

(i had applied some trigonometry identities),

sin(A + 2c) = (1 - (1/2)(cosA)^2),

which leads to:

A + 2c = asin(1 - (1/2)(cosA)^2);

A - 2c = 2A - asin(1 - (1/2)(cosA)^2);

sinB = sin((Pi/2 + A - 2c)/2) =

sinB = √(1 + sin(2A - asin(1 - (1/2)(cosA)^2))),

(note: B > 0); so for A0 = Pi/2 - Pi/3 = Pi/6,

sinB0 = sqrt((1 + sin(Pi/3 - asin(5/8)))/2) = 0,825693909,

B0 = 0,971431172 rad;

b0 = Pi/2 - B0 = 0.599365154 rad,

AS1(O1,2r,2b0) = b0 (2r)^2 = 4b0r^2 = 2,397460617 r^2

AS2(O2,2r,(2/3)Pi) = (1/3)Pi = 1.047197551*r^2

2At(O1O2P) = 2(1/2)|O1P||O2M| = 2(r^2)sin(b0) =

2(r^2)sin(b0) = 2At(O1P2P) = 1.128236797*r^2;

Ash = 0.222026269(r^2) = k(r^2) =>

k = 0.222026269;

ceil(100k) = 22

Antonio Fanari - 6 years, 9 months ago

Yeah! Same method , just I considered the triangle $\ce{O1O2P}$ to find $a$ and then $\theta$ !

Aniket Sanghi - 4 years, 9 months ago

Steven Zheng
Jul 29, 2014

I used the sine law to determine an angle first. The geometry becomes elementary thereafter.

Of course I myself have done like that

Ronak Agarwal - 6 years, 10 months ago

Niranjan Khanderia
Aug 2, 2014

$\because~of~symmetry,~we~shall~only~consider~the ~right~half.$
$Extend~O_1O_2~to~meet~the~circles~at~~A.$
$Small~circle~radius~O_2C~makes~~ \angle 60^o~with~AO_2.$
$Extend~O_2C~ to~meet~big~circle~at~B.$

$Applying~Sin~Rule~to~\triangle ~O_1O_2B,~~$
$\angle O_2BO_1 = Sin^{-1 }\{ (r * Sin120^o) / (2r) \} = 25.66^o.$
$\angle O_2O_1B = 60 - 25.66 = 34.34^o.$

$Area~ ABO_1 = Area~ AB'O_1$

$\color\red {The ~Area~ABC = Area~ ABO_{1} -Area~O_{1}O_{2}B-Area~ACO_2}$

$\color\red {Area~ ABO_1} = 34.34^o/360^o * \pi * (2r)^2 =\color\green{ \boxed {1.199 * r^2}}$

$So~the~\color\red{Area~O_{1}O_{2}B} = \frac{1}{2} * (2r) * (r * Sin34.34^o) = \color\green{ \boxed {0.564 * r^2}}.$

$\color\red {Area~ ACO_2} = 60^o/360^o * \pi * r^2 = \color\green{ \boxed {0.523 * r^2}}$

$\color\green {shaded ~Area~ABC = 1.199 - 0.564 - 0.523 =.112 * r^2 }$

$\boxed{ A = \lfloor 100 * 2 * .112 \rfloor = 22}$

how do you get 34.34 degrees?

Danielle Man Lin - 6 years, 10 months ago

It is given. But now I have change the order to make it clear.

Niranjan Khanderia - 6 years, 9 months ago

Find the area

Also try Let's play pool .

The answer is 22.

3 solutions

0 pending reports