find the area
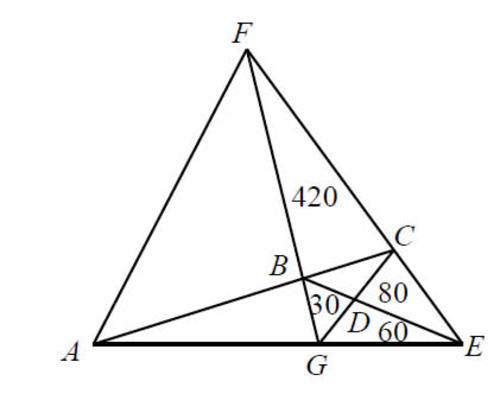A triangle is divided into seven triangles. The areas of four of them are
4
2
0
c
m
2
,
8
0
c
m
2
,
6
0
c
m
2
and
3
0
c
m
2
as shown in the diagram on the right. Find the area of
△
A
E
F
, in
c
m
2
The answer is 1512.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Could you please explain why these proportions are equal?
Log in to reply
We note that △ BCE and △ BCF have the same height from their base EF, therefore the ratio of their areas is equal to the ratio of their bases CE and CF.
⇒ 4 2 0 z + 8 0 = C F C E
Similarly, △ GCE and △ GCF have the same height from their base EF and therefore,
⇒ z + 3 0 4 2 0 8 0 + 6 0 = C F C E = 4 2 0 z + 8 0
Similar logic for the other equation.
did the same way!!
the key is that ratio of areas of 2 triangles sharing a common vertex = base ratio of the two, provided the bases are opposite to common vertex. using this we can get through it.
Yes it is !
Let the areas of △ A B F , △ A B G and △ B C D be x , y and z respectively. Then, we have:
4 2 0 z + 8 0 = z + 3 0 + 4 2 0 8 0 + 6 0 = z + 4 5 0 1 4 0
( z + 8 0 ) ( z + 4 5 0 ) = 1 4 0 × 4 2 0
z 2 + 5 3 0 z − 2 2 8 0 0 = 0 ⇒ z = 4 0
Now, we have: 8 0 + 6 0 y + 4 0 + 3 0 = 3 0 + 6 0 y ⇒ y = 1 2 6
And: 1 2 6 + 3 0 + 4 0 + 8 0 + 6 0 x + 4 2 0 = 4 0 + 8 0 4 2 0 ⇒ x = 7 5 6
The area of △ A E F = 7 5 6 + 1 2 6 + 4 0 + 4 2 0 + 3 0 + 8 0 + 6 0 = 1 5 1 2