Find the area-No Parabolem!
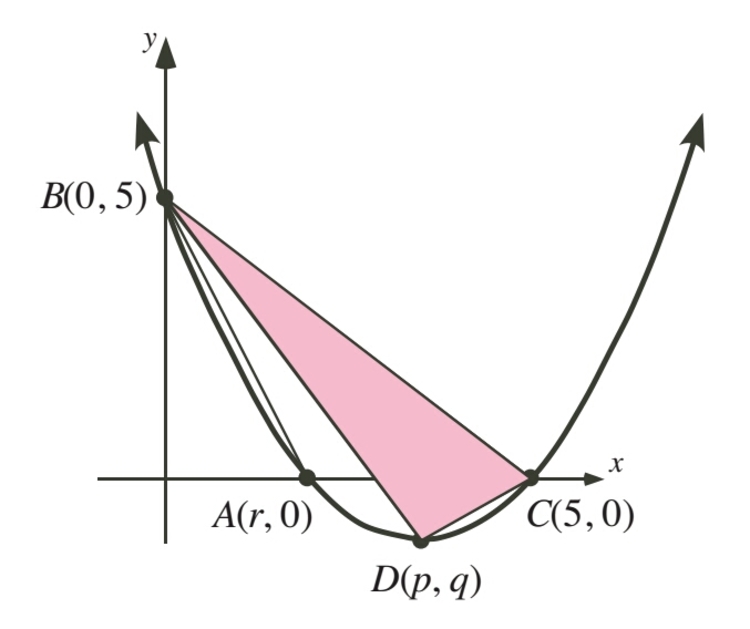 In the diagram ,
is the vertex of the parabola.The parabola cuts the
-axis at
and
. The area of
is
.
In the diagram ,
is the vertex of the parabola.The parabola cuts the
-axis at
and
. The area of
is
.
Determine the area of .
The answer is 3.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Given that area of △ A B C = 5 .
Taking the base as A C and height O B ( O is the origin), we have,
⟹ ⟹ 2 1 ⋅ ( 5 − r ) ⋅ 5 = 5 5 − r = 2 r = 3
So the point A ≡ ( 3 , 0 ) .
We can observe that the axis of this parabola is parallel to the y − a x i s and hence the abscissa of its vertex will be exactly in between x = 3 and x = 5 , thus giving p = 4 .
There are three points given to us on the parabola. Using the equation y = A x 2 + B x + C for the equation of this parabola and plugging in the corresponding values of x and y from the three given points A , B and C , we get,
A = 3 1 , B = − 3 8 , C = 5
So, our equation of parabola becomes,
y = 3 x 2 − 3 8 x + 5
Plugging in for x = 4 we get y = − 3 1 .
Thus, the coordinates of point D ( p , q ) are ( 4 , − 3 1 ) .
Hence, the area of △ D B C is,
Δ = = 2 1 ∣ ∣ ∣ ∣ ∣ ∣ 0 4 5 5 − 1 / 3 0 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ 3 1 0 = 3 . 3 3