Find the side length of the equilateral triangle
Shown below is an equilateral
△
A
B
C
of side length
s
. A point
P
is inside the triangle such that
A
P
=
1
,
B
P
=
3
and
C
P
=
2
. Find
s
.

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
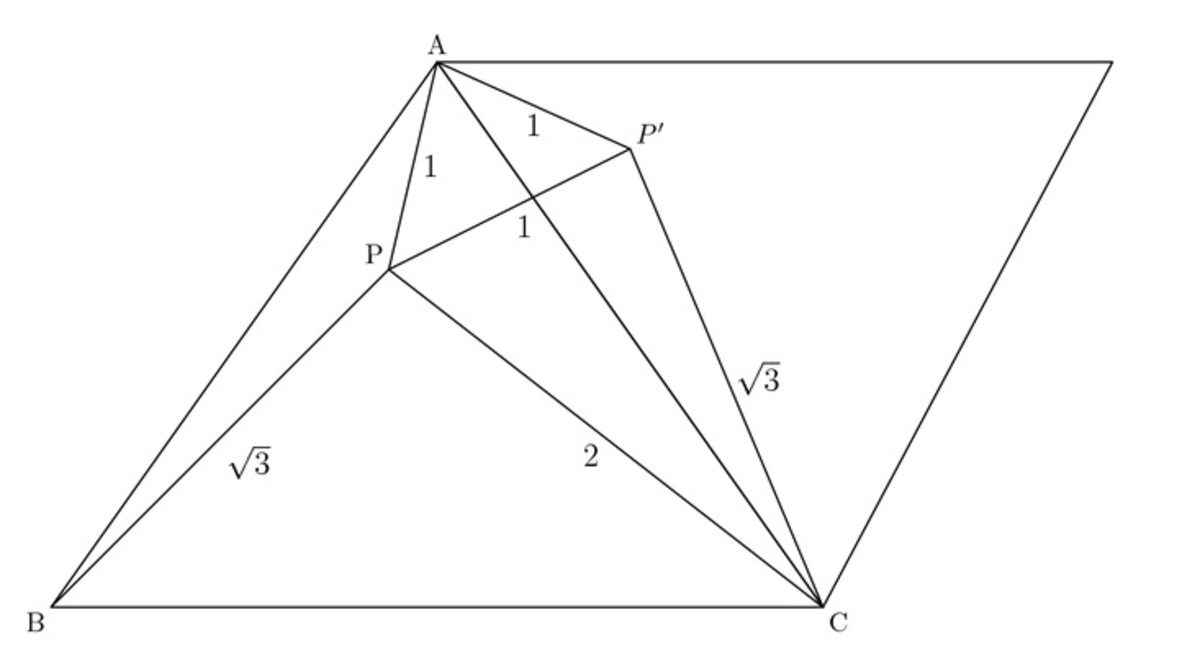 Begin by rotating
△
A
B
C
by
6
0
∘
about
A
, such that in
△
A
′
B
′
C
′
,
B
′
=
C
. We see that
t
r
i
a
n
g
l
e
A
P
P
′
is equilateral triangle with side length
1
, meaning that
∠
A
P
P
′
=
6
0
∘
. We also see that
△
C
P
P
′
is a
3
0
∘
−
6
0
∘
−
9
0
∘
right triangle, meaning that
∠
C
P
P
′
=
6
0
∘
. Thus, by adding the two together, we see that
∠
A
P
C
=
1
2
0
∘
. We can now use the law of cosines as following:
Begin by rotating
△
A
B
C
by
6
0
∘
about
A
, such that in
△
A
′
B
′
C
′
,
B
′
=
C
. We see that
t
r
i
a
n
g
l
e
A
P
P
′
is equilateral triangle with side length
1
, meaning that
∠
A
P
P
′
=
6
0
∘
. We also see that
△
C
P
P
′
is a
3
0
∘
−
6
0
∘
−
9
0
∘
right triangle, meaning that
∠
C
P
P
′
=
6
0
∘
. Thus, by adding the two together, we see that
∠
A
P
C
=
1
2
0
∘
. We can now use the law of cosines as following:
s 2 = ( A P ) 2 + ( C P ) 2 − 2 ( A P ) ( C P ) ( cos ∠ A P C )
s 2 = 1 + 4 − 2 ( 1 ) ( 2 ) ( 2 − 1 )
s 2 = 5 − 4 ( 2 − 1 )
s = 7 answer
Nice solution! One note: The title of the problem asks for the area of the triangle, but finaly the question is about its side :)
Log in to reply
@Thanos Petropoulos Thank you for checking my mistake. I edited the title for clarity.
Log in to reply
@Marvin Kalngan You wellcome! It is a very nice problem among those that can be solved by rotation.
Let the centroid of △ A B C be O ( 0 , 0 ) , the origin of the x y -plane. Then A ( 0 , 3 s ) , B ( − 2 s , − 2 3 s ) , and C ( 2 s , − 2 3 s ) . Let P ( x , y ) . Then we have
⎩ ⎪ ⎨ ⎪ ⎧ x 2 + ( y − 3 s ) 2 = 1 ( x + 2 s ) 2 + ( y + 2 3 s ) 2 = 3 ( x − 2 s ) 2 + ( y + 2 3 s ) 2 = 4 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
From ( 3 ) − ( 2 ) : − 2 s x = 1 ⟹ x = − 2 s 1 .
From ( 2 ) − ( 1 ) :
s x + 4 s 2 + 3 s y + 1 2 s 2 + 3 2 s y − 3 s 2 − 2 1 + 3 s y ⟹ y = 2 = 2 = 2 3 s 5
Substitute x and y in ( 1 ) :
4 s 2 1 + ( 2 3 s 5 − 3 s ) 2 4 s 2 1 + 1 2 s 2 2 5 − 3 5 + 3 s 2 3 s 2 7 − 3 8 + 3 s 2 s 4 − 8 s 2 + 7 ( s 2 − 1 ) ( s 2 − 7 ) ⟹ s = 1 = 1 = 0 = 0 = 0 = 7 Since s > 1
Let ∠ P C A = α , ∠ P C B = 6 0 ° − α
Then
cos α = 4 s s 2 + 3
cos ( 6 0 ° − α ) = 4 s s 2 + 1
Solving we get
sin α = 4 3 s s 2 − 1
So, cos 2 α + sin 2 α = 1 ⟹ 1 6 s 2 ( s 2 + 3 ) 2 + 4 8 s 2 ( s 2 − 1 ) 2 = 1
⟹ s 4 − 8 s 2 + 7 = 0 ⟹ s = 1 , 7
Obviously s can't be 1 , since then ∣ P A ∣ + ∣ A C ∣ = 1 + 1 = 2 = ∣ P C ∣
Therefore s = 7 .
Begin by rotating the hole figure by 6 0 ∘ clockwise, about C , as shown below.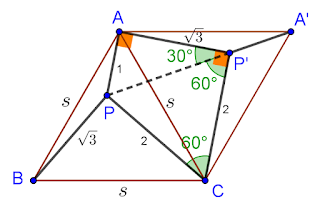
C P = C P ′ = 2 and ∠ P C P ′ = 6 0 ∘ , hence △ P C P ′ is equilateral.
Thus, P P ′ = 2 . Consequently, △ A P P ′ is a 1 - 3 - 2 triangle, i.e. a 3 0 ∘ - 6 0 ∘ - 9 0 ∘ right triangle, with ∠ A P ′ P = 3 0 ∘ .
Now, ∠ A P ′ C = ∠ A P ′ P + ∠ P P ′ C = 3 0 ∘ + 6 0 ∘ = 9 0 ∘ By Pytghagorean theorem on △ A P ′ C , A C 2 = A P ′ 2 + P ′ C 2 ⇒ s 2 = 3 2 + 2 2 = 7 ⇒ s = 7