Find the area of the equilateral triangle inscribed in a circle

Express the equation of the circle in the form x^2 + y^2 + 2gx + 2fy + c = 0

Completing the square of the equation above we see that the square of the radius of such a circle is (g^2 + f^2 -c) The area of the equilateral triangle is simply (3 sqrt(3)/4) r^2

Which comes to (3*sqrt(3)/4)(g^2 + f^2 − c) sq units.

Relevant wiki: Completing the Square - Basic

$x^2+y^2+12x+16y+60=0$

Rearrange and complete the square.

$x^2+12x+36+y^2+16y+64=-60+36+64$

$(x+6)^2+(y+8)^2=40$

We can see that $r^2=40$ or $r=\sqrt{40}$ .

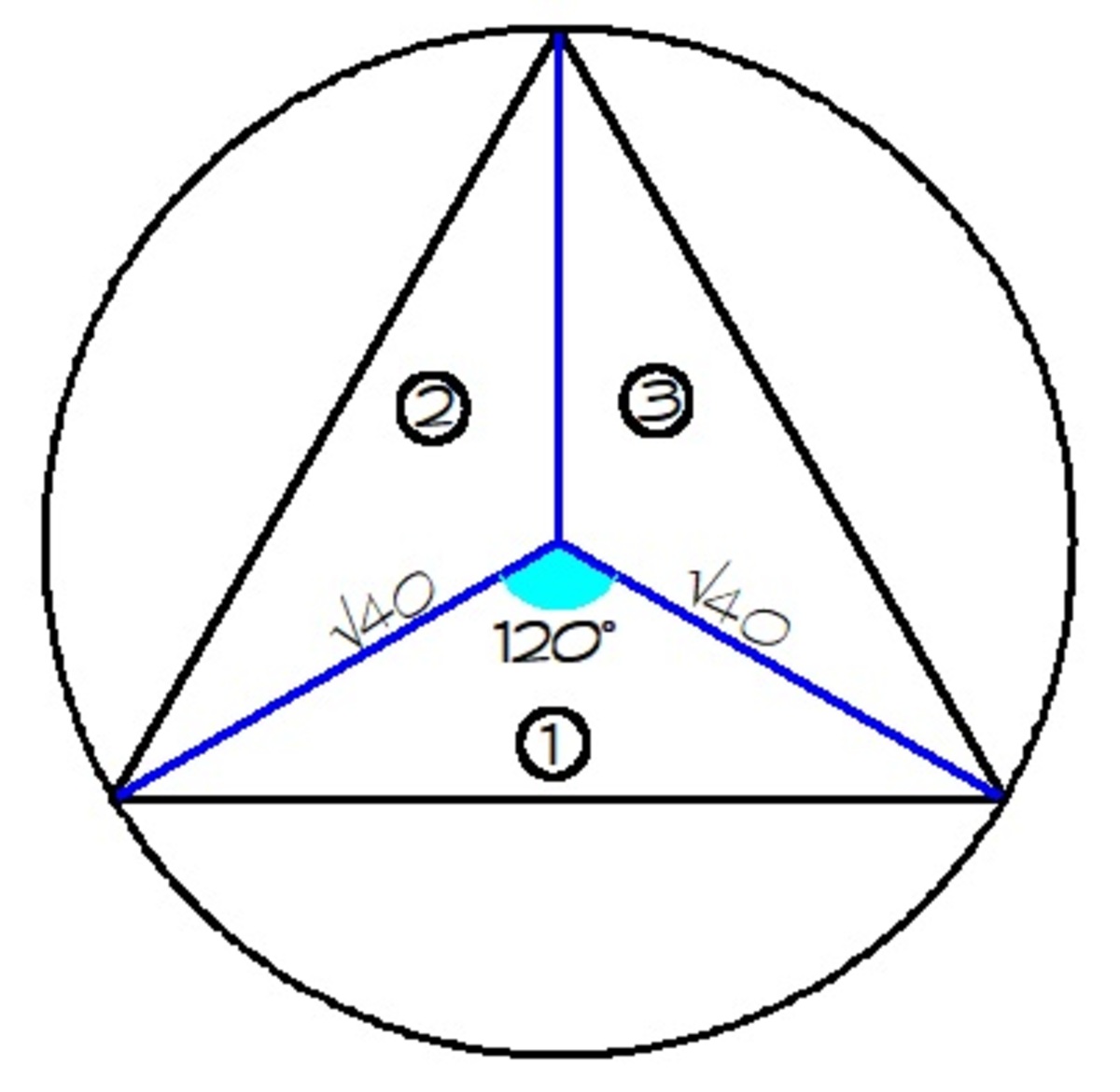
Consider my figure on the right. The equilateral triangle is composed of three congruent isosceles triangles.

$A=3\left(\dfrac{1}{2}\right)(r^2)(\sin 120)=\dfrac{3}{2}(40)(\sin 120)\approx$ $\boxed{51.961}$

Note:

The formula used is $A=\dfrac{1}{2}ab \sin C$ . I multiplied it by three because I divided the equilateral triangle into three isosceles triangles.