Find the area of the intersection between two circles
Geometry
Level
3
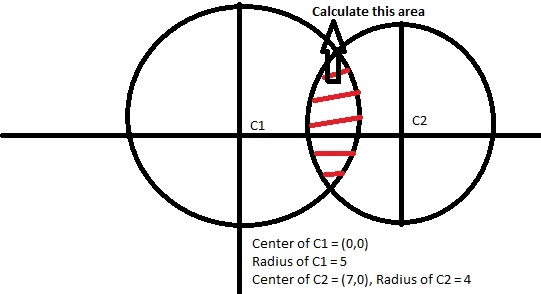
Find the area of intersection of two circles as shown in the figure above. Round of to 1 decimal.
The answer is 7.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Equation of the two circles x x + y y = 25 -- C1
Circle C2 (x-7) (x-7) + y y = 16
x x - 14x + 49 +y y = 16 x x - 14x +y y = - 33
Solving for intersection points A and B of the two circles
14x - 49 =9 14x = 58 x = 4.14 y = +/- 2.79 Co-ords of A are (4.14, 2.79) and of B are (4.14 ,-2.79)
Length of the chord AB = 5.58
Angle subtended by the chord AC1B = 2 * invsin(2.79/5) = 67.84 degrees
Area of the sector C1AB = (67.84/360) 25 22/7 = 14.8 sqcm Area of the triangle C1AB = 11.58
Area of the segment 1 =14.8 - 11.58 = 3.22 sqcm
Angle subtended the chord on circle 2 AC2B = 2 * 44.2267712 = 88.44 degrees Area of the sector AC2B = (88.44/360) 16 22/7 = 12.35 sqcm Area of the triangle AC2B = 7.999 sqcm Area of the segment 2 = 12.35 - 7.999 = 4.35 sqcm
Total intersected area = Area of Segment 1 + Area of Segment 2 = 7.57 sqcm