Find the area of the shaded part.
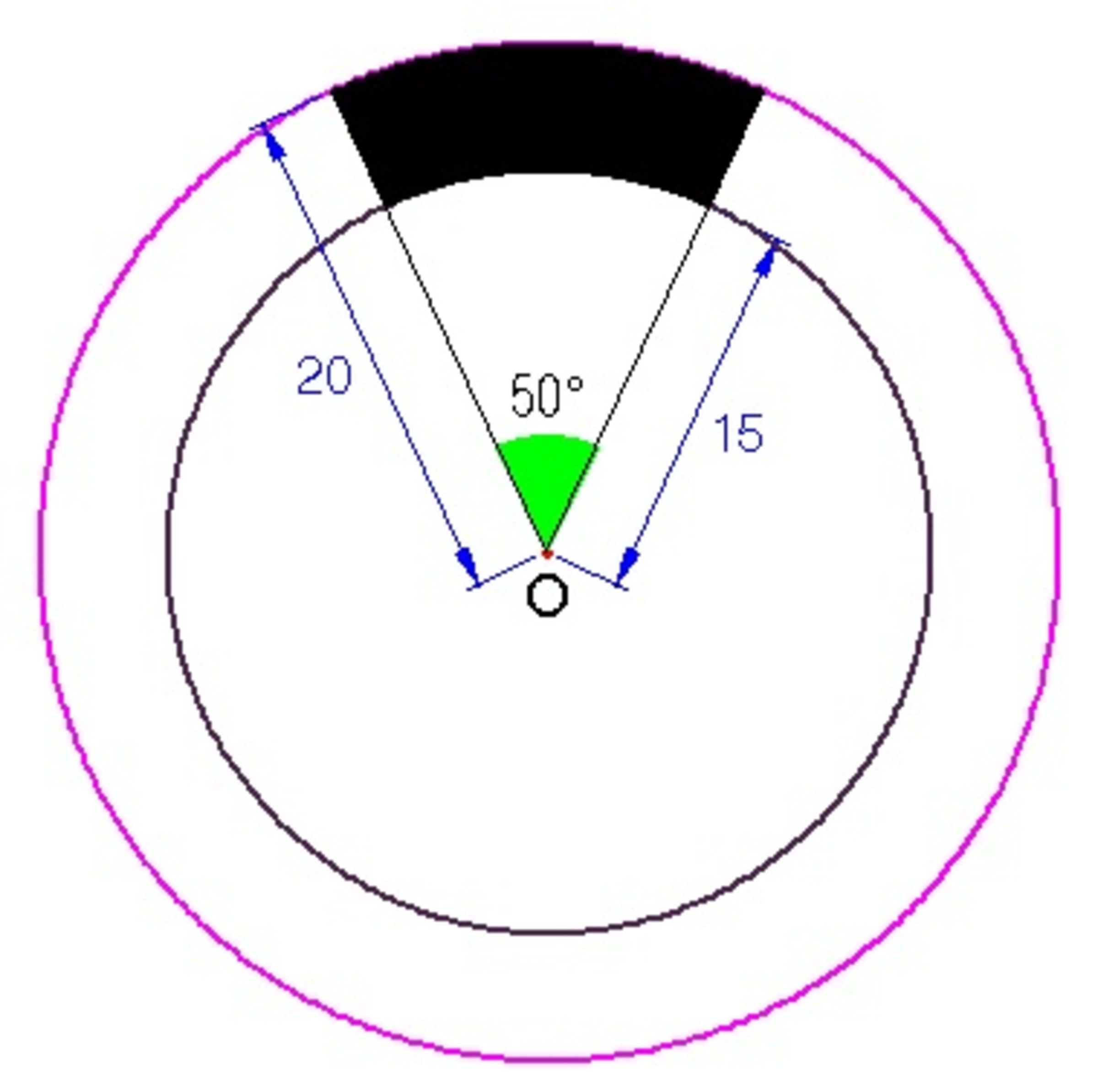 Shown in the above figure are two concentric circles with center at point
whose radii are
and
, respectively. Given that the central angle is
, find the area of the shaded part. Give your answer correct to two decimal places.
Shown in the above figure are two concentric circles with center at point
whose radii are
and
, respectively. Given that the central angle is
, find the area of the shaded part. Give your answer correct to two decimal places.
Use the approximation
The answer is 76.36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The area of the shaded part is the difference of the areas of two sectors of a circle. Let θ be the measure of the central angle, A s be the area of the shaded part, R be the radius of the big circle and r be the radius of the small circle..
Then,
A s = 3 6 0 θ π ( R 2 − r 2 ) = 3 6 0 5 0 ( 1 1 3 3 5 5 ) ( 2 0 2 − 1 5 2 ) ≈ 7 6 . 3 6