find the area of the smallest circle
Geometry
Level
3
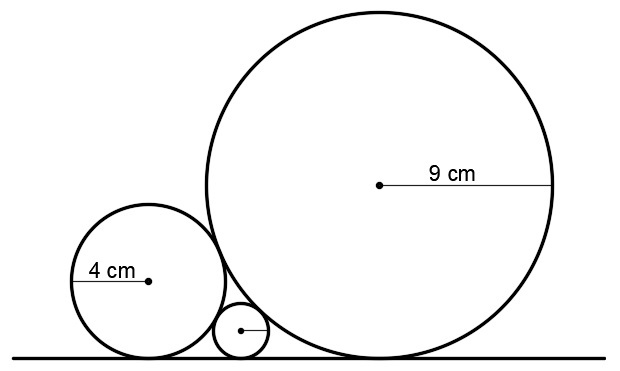Three circles are externally tangent to each other and to a line as shown in the figure. If the radius of one circle is 4 cm and the other is 9 cm, find the area of the smallest circle in square centimeters.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Drop a perpendicular from the center of the large circle, intersecting the horizontal line at point A. Do the same from the center of circle wiyh radius 4 to the horizontal line, denoting this by B. Finally, do the same for the small circle, calling the intersection point C. Draw a line through the center of circle of radius 4 parallel to the horizontal line at bottom and intersecting the altitude though point A, calling the intersection point D.The distance between the centers of the circles of radii 4 and 9 is equal to 13. The distance from the center of circle with radius 9 and D is 9 - 4 - 5. Then by the Pythagorean theorem, BA = 12. Let BC = x and CA = 12 - x.Then we have two right triangles with the center of the small circle as a vertex for each. This results in the following 2 equations by Pythagoras: (1) (4 + r)^2 = x^2 + (4 - r)^2, and (2) (9+ r)^2 = (12 - x)^2 + (9 - r)^2, where r = radius of small circle. Solving these equations, we have: 16r = x^2, and 36r = (12 - x)^2. This results in x = 24/5, and r = 1.44. Then the area of the small circle = pi r^2 = 2.0736 pi. Ed Gray