Find the area of the yellow region...
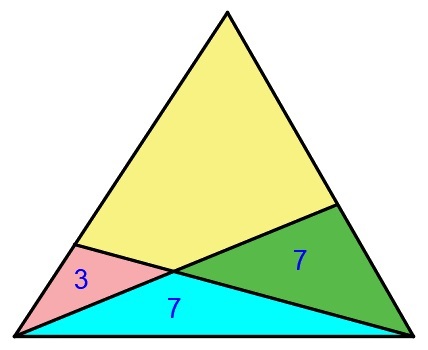 A triangle is divided into four parts. The areas of some parts are written inside each triangle. Find the area of the yellow region.
A triangle is divided into four parts. The areas of some parts are written inside each triangle. Find the area of the yellow region.
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
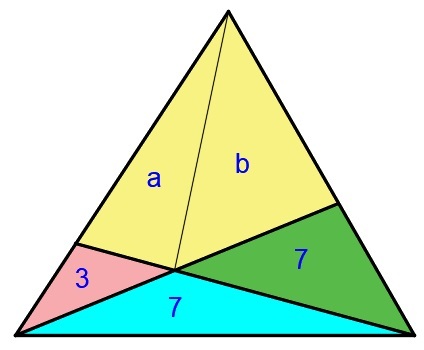 This can be solved by proving the
Ceva's Theorem
This can be solved by proving the
Ceva's Theorem
3 3 + 7 = a a + b + 7 ⟹ 3 1 0 = a a + b + 7 ⟹ 7 a = 3 b + 2 1 ( 1 )
b a + b + 3 = 7 7 + 7 ⟹ b a + b + 3 = 2 ⟹ a = b − 3 ( 2 )
Solving ( 1 ) and ( 2 ) , we get
a = 1 0 . 5 and b = 7 . 5 .
The desired area is 7 . 5 + 1 0 . 5 = 1 8 .
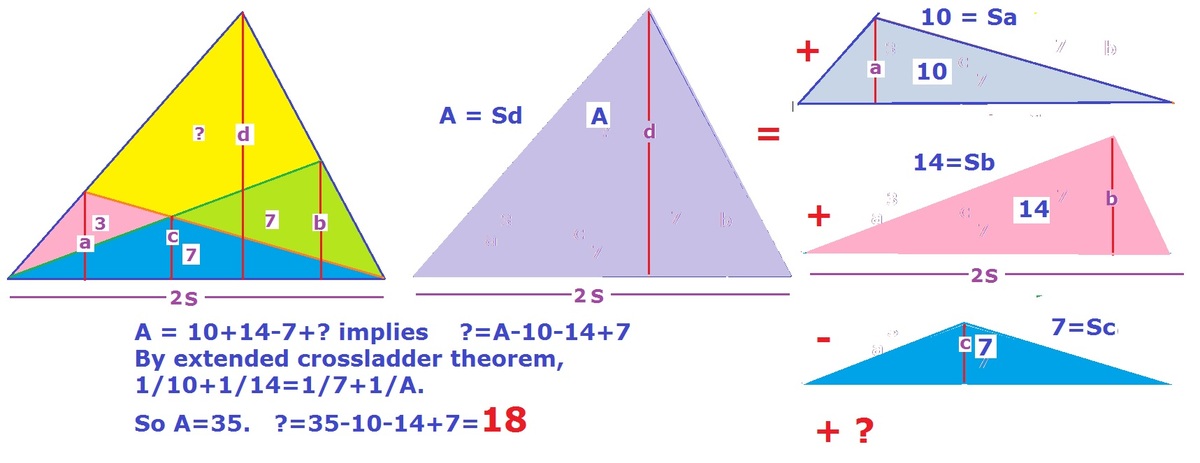
Now divide the yellow region into x = [ A E D ] and y = [ A D F ] as shown. Note that △ A B D and △ A D F are sharing the same height h 3 . Therefore,
[ A D F ] [ A B D ] y 3 + x ⟹ y = D F B D = 1 = x + 3 Note that B D = D F
Similarly, △ A E D and △ A D C are sharing the same height h 4 .
[ A D C ] [ A E D ] 7 + y x 7 x 7 x ⟹ x ⟹ y = D C E D = 7 3 = 2 1 + 3 y = 2 1 + 3 x + 9 = 7 . 5 = 7 . 5 + 3 = 1 0 . 5 Note that y = x + 3
Therefore the area of the yellow region x + y = 7 . 5 + 1 0 . 5 = 1 8 .