Find the Blue Area
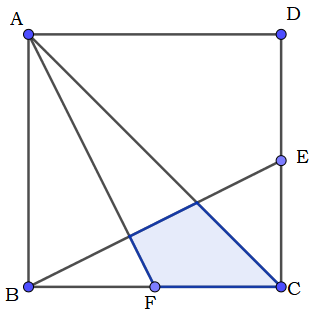
In the figure above the square has side length of . The points and are the midpoints of the sides and respectively.
The blue area can be represented as , where and are co-prime integers. Find .
The answer is 67.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
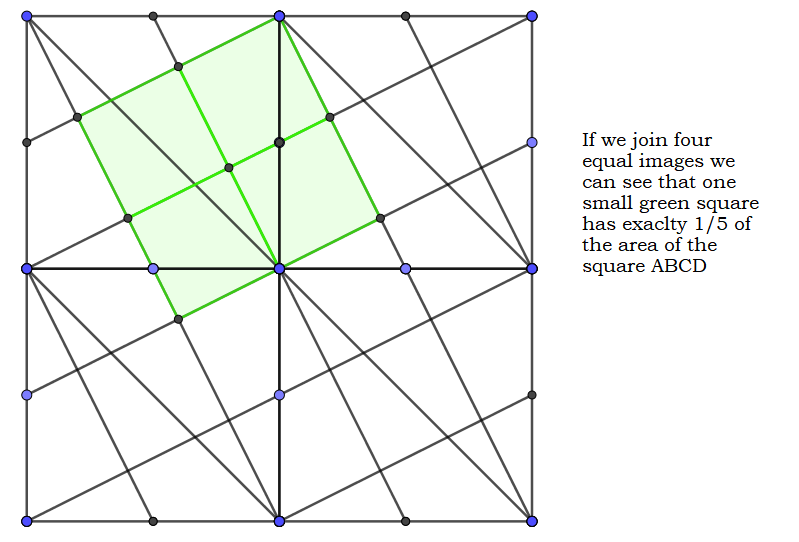
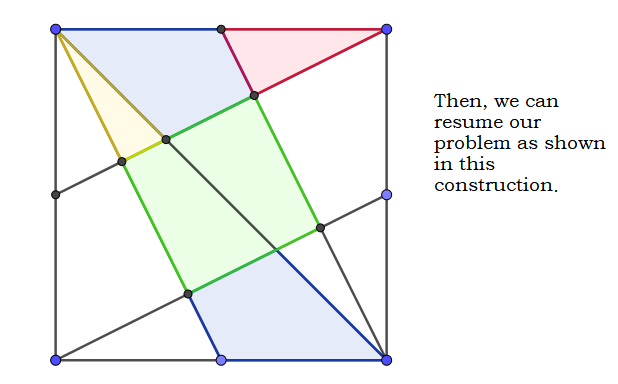
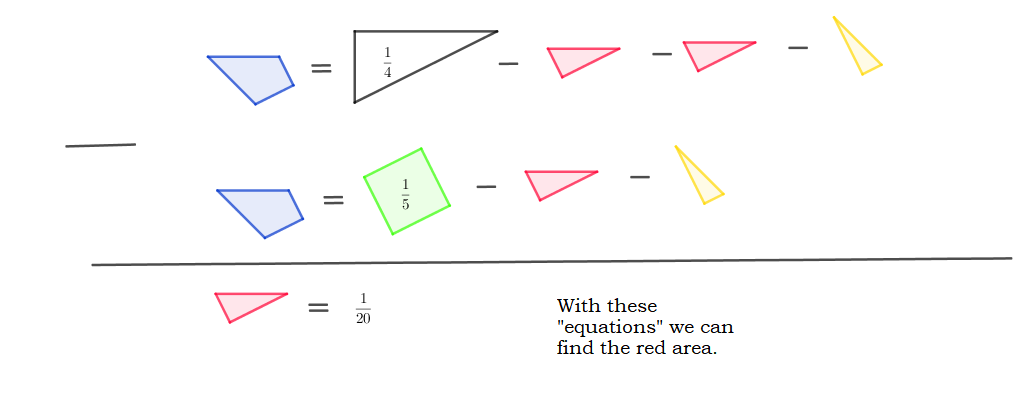
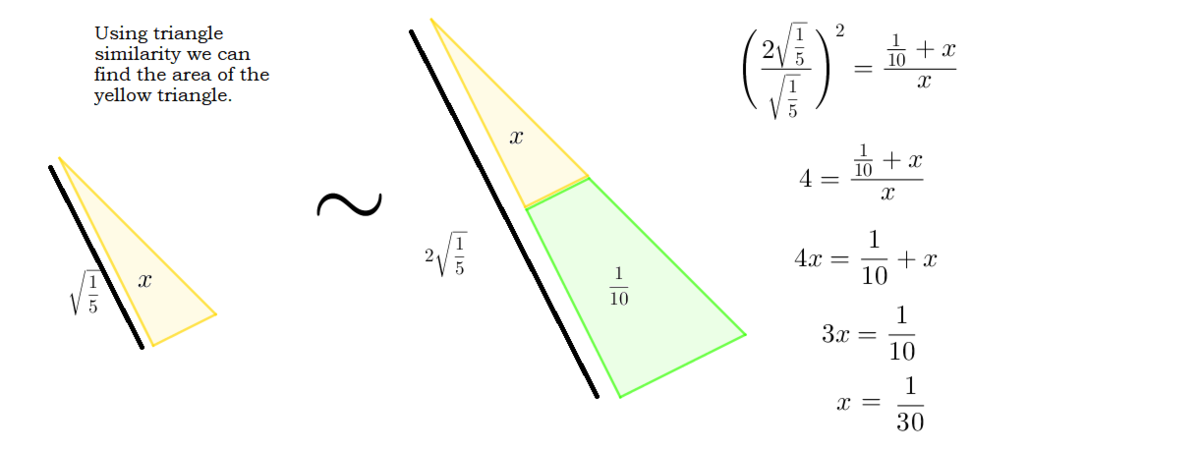
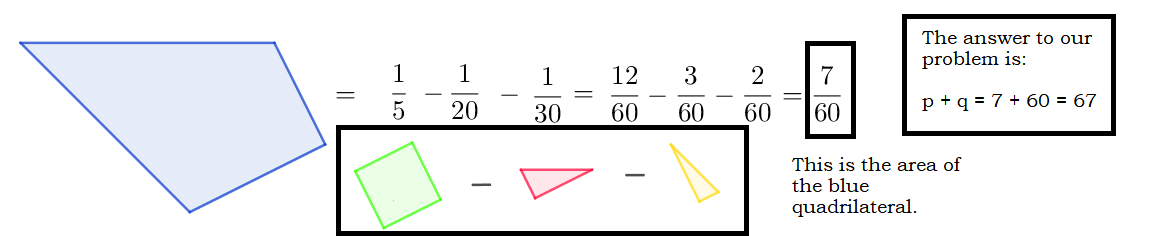
On an analytical aspect, we'll use coordinate geometry
Here in the above figure , we use the two point formula to find the equations for the green, yellow and red line and their equations are y = 2 x ⟶ ( 1 ) , y = − 2 x + 1 ⟶ ( 2 ) , y = − x + 1 ⟶ ( 3 )
From the above figure its very clear that the green line bisects red and yellow line at the points p and q ; On solving the equations ( 1 ) and ( 3 ) we'll obtain the value of point P to be ( 3 2 , 3 1 )
similarly on solving the equations ( 1 ) and ( 2 ) the value of point Q is found to be ( 5 2 , 5 1 )
so finally we have obtained the points for the vertices of the given blue shaded region P , Q , F , C . To find the area of the shaded region we make use of the shoelace formula, once we plug the points into that particular formula we'll obtain the area of the blue shaded region to be 6 0 7