Find the challenging infinite sum
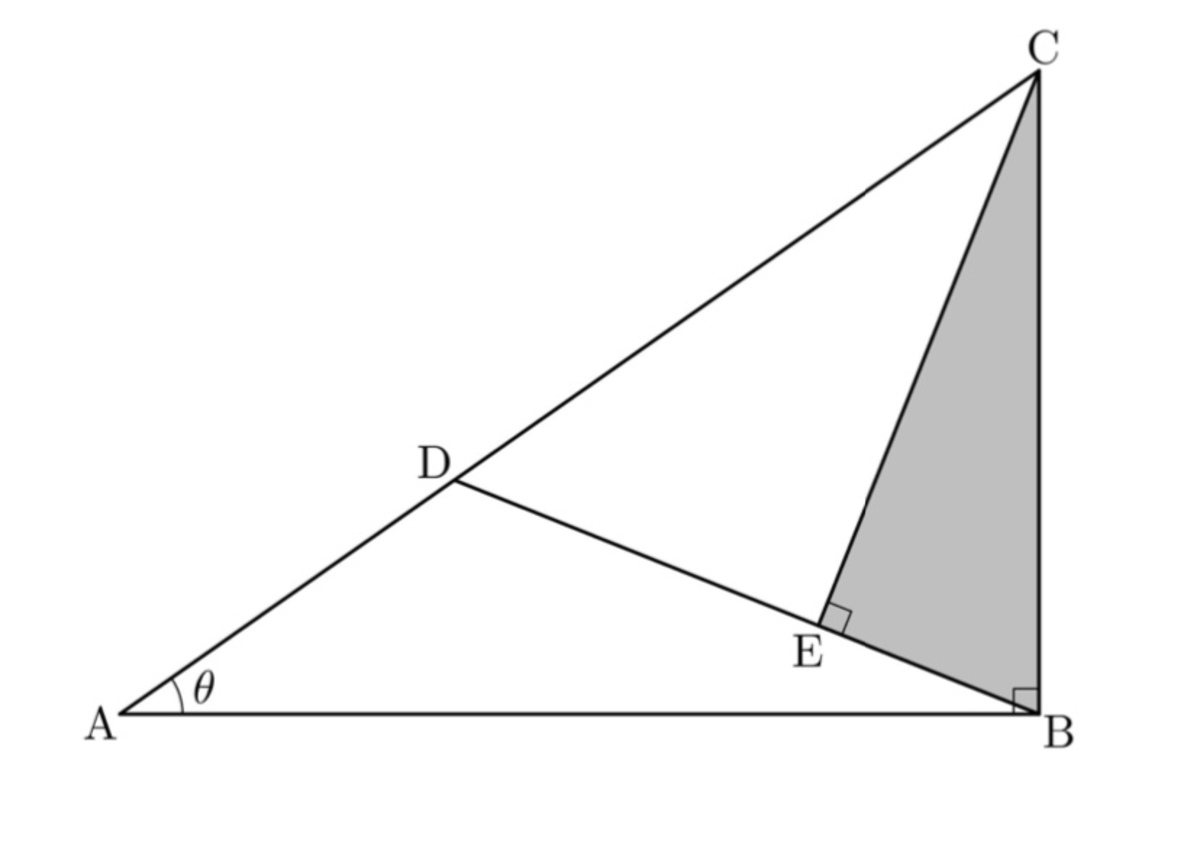
In the diagram above, is a right triangle where and . Point is on the hypotenuse such that . Point is on such that is a right triangle whose hypotenuse is and whose area is . Repeat this process, starting with picking a point on the hypotenuse such that . Let be the area of the th right triangle.
The sequence of numbers , for , is such that the limit exists and is nonzero. Denote as
where .
Find .
Notation: denotes the floor function .
The answer is 18458750876.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Thus, if θ n (for n ≥ 0 ) is the corresponding angle of the n th right-angled triangle, then tan θ n + 1 = 1 − t t tan θ n and hence tan θ n = ( 1 − t t ) n tan θ n ≥ 0 Moreover, if x n is the corresponding side of the n th triangle, then x n + 1 = x n tan θ n cos θ n + 1 and the area of the n th triangle is S n = 2 1 x n 2 tan θ n so that S n + 1 = 2 1 x n + 1 2 tan θ n + 1 = 2 1 x n 2 tan 2 θ n cos 2 θ n + 1 tan θ n + 1 = S n tan θ n tan θ n + 1 cos 2 θ n + 1 = S n ( 1 − t t ) 2 n + 1 tan 2 θ cos 2 θ n + 1 and so ( t 1 − t ) ( n + 1 ) 2 S n + 1 ( t 1 − t ) ( n + 1 ) 2 tan 2 ( n + 1 ) θ S n + 1 = ( t 1 − t ) n 2 S n tan 2 θ cos 2 θ n + 1 = ( t 1 − t ) n 2 tan 2 n θ S n cos 2 θ n + 1 so we deduce that S n = S 0 ( 1 − t t ) n 2 tan 2 n θ j = 1 ∏ n cos 2 θ j = 2 1 ( 1 − t t ) n 2 tan 2 n + 1 θ j = 1 ∏ n cos 2 θ j Thus it follows that θ → 0 + lim θ 2 n + 1 S n = 2 1 ( 1 − t t ) n 2 so we deduce that a n = 2 n + 1 b n = 2 1 ( 1 − t t ) n 2 n ≥ 0 Since b 0 = 2 1 and we require the sum of the b n to be less than 2 1 , we must be ignoring the original triangle A B C in these calculations, and we need to find 0 < t < 1 such that 1 = 2 n = 1 ∑ ∞ b n = n = 1 ∑ ∞ q n 2 = 2 1 ( ϑ 3 ( 0 , q ) − 1 ) where q = 1 − t t . Solving this equation numerically gives q = 0 . 7 0 5 3 4 6 6 8 1 3 7 9 8 0 6 9 8 9 6 3 6 3 7 9 7 0 6 3 9 4 . . . t = 0 . 4 1 3 6 0 8 9 6 8 2 4 1 6 4 0 1 3 6 3 5 0 6 1 7 7 2 4 0 5 3 and hence X = n = 1 ∑ ∞ a n b n = 2 1 n = 1 ∑ ∞ ( 2 n + 1 ) q n 2 = 1 . 8 4 5 8 7 5 0 8 7 6 7 7 4 4 7 2 0 0 8 4 7 9 9 2 8 9 1 7 8 and hence ⌊ 1 0 1 0 X ⌋ = 1 8 4 5 8 7 5 0 8 7 6 Although I am not immediately aware of a closed form for X , it is easy to find X to the required degree of accuracy. Since q < 4 3 , we can show that ( 2 n + 1 ) q n ≤ 7 q 3 < 3 n ∈ N and hence n = N + 1 ∑ ∞ ( 2 n + 1 ) q n 2 ≤ 3 n = N + 1 ∑ ∞ q n ( n − 1 ) ≤ 3 q N n = N + 1 ∑ ∞ q ( n − 1 ) 2 ≤ 3 q N n = N 2 ∑ ∞ q n = 1 2 ( 4 3 ) N ( N + 1 ) Thus n = N + 1 ∑ ∞ ( 2 n + 1 ) q n 2 < 5 × 1 0 − 1 1 provided that 1 2 ( 4 3 ) N ( N + 1 ) < 5 × 1 0 − 1 1 or N ( N + 1 ) > lo g 1 0 3 4 1 1 + lo g 1 0 2 . 4 = 9 1 . 0 9 , and hence provided that N ≥ 1 0 . Thus we can get 1 0 decimal place accuracy for X by calculating n = 1 ∑ 1 0 ( 2 n + 1 ) q n 2