Find the coloured area
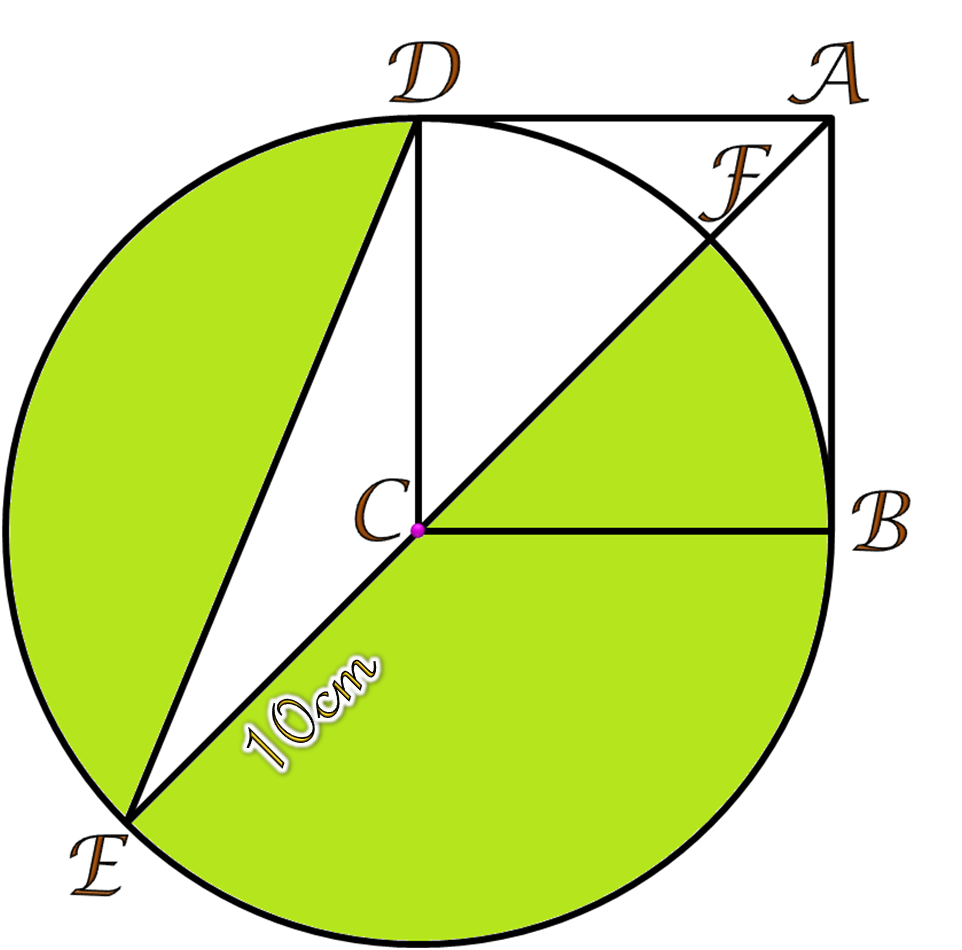
A B C D is square and C is the center of the circle. Given that C E = 1 0 cm and D E C is a triangle. Find the area of the shaded region (in cm 2 ).
Give your answer to 2 decimal places.
The answer is 239.53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Area = Area of circle − area of pie slice D C F − area of triangle D E C .
Area = 1 0 0 π − 3 6 0 4 5 ⋅ 1 0 0 π − 2 ⋅ 2 1 ⋅ 1 0 s i n ( 2 2 . 5 ) ⋅ 1 0 c o s ( 2 2 . 5 ) = 2 3 9 . 5 3

The area of the shaded region is equal to the area of a semicircle plus the area of a circular segment. The area of the semicircle is 2 1 π ( 1 0 2 ) ≈ 1 5 7 . 0 8 . The area of the circular segment is equal to the area of the circular sector minus the area of the triangle, we have 3 6 0 1 3 5 ( π ) ( 1 0 2 ) − 2 1 ( 1 0 2 ) ( sin 1 3 5 ) ≈ 8 2 . 4 5 . So the desired area is 1 5 7 . 0 8 + 8 2 . 4 5 = 2 3 9 . 5 3