Find the Compression -2!
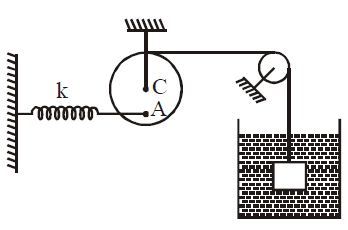 A cubical block of volume
and density
is placed inside a liquid of density
and attached to a spring of spring constant
as shown in the figure. Assuming ideal spring and pulley and spring is attached at
which is at
from center. The compression in the spring at equilibrium is:
A cubical block of volume
and density
is placed inside a liquid of density
and attached to a spring of spring constant
as shown in the figure. Assuming ideal spring and pulley and spring is attached at
which is at
from center. The compression in the spring at equilibrium is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let T be the tension . Let B be the buoyant force.
balancing forces
T + B = m g
T = 2 ρ V g
balancing torque
T R = k x 2 R
x = k 4 ρ V g