Find the diagonal
The perimeter of a rhombus of 96 cm and obtuse angle of 1 2 0 ∘ .
Find the lengths of its diagonals.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
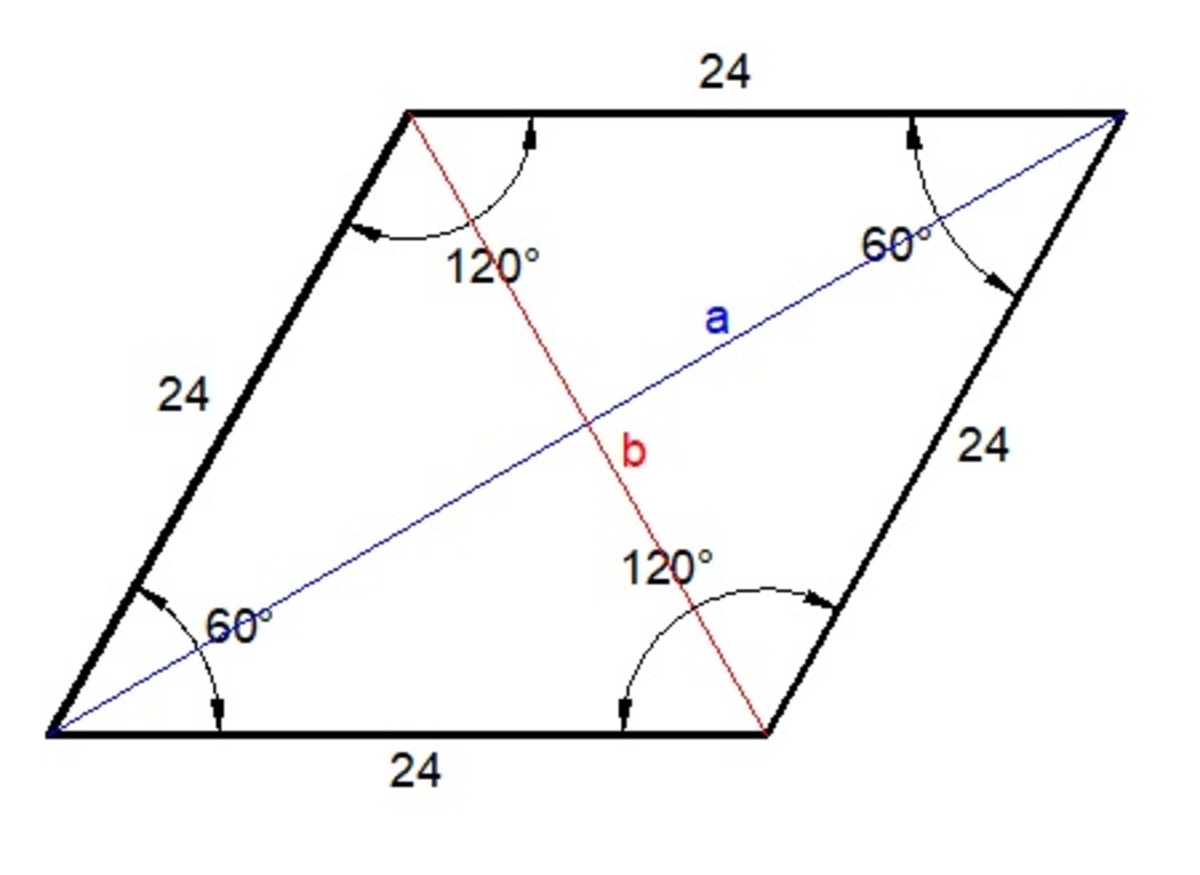 Consider the diagram on the left.
Consider the diagram on the left.
By law of cosines, we have
a 2 = 2 4 2 + 2 4 2 − 2 ( 2 4 ) ( 2 4 ) ( cos 1 2 0 ) ⟹ a = 4 1 . 5 7
By law of cosines again, we have
b 2 = 2 4 2 + 2 4 2 − 2 ( 2 4 ) ( 2 4 ) ( cos 6 0 ) ⟹ b = 2 4
No other calculation apart from dividing 96 into 4 equal side length needed. If the obtuse angle is 120°, then said rhombus must have made up from combining 2 equilateral triangle together, so its shorter diagonal must be 24.