Find the Electric field!
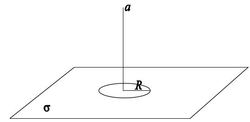 An infinitely large surface of uniform charge density
σ
has a disc of radius
R
cut out (see figure). The magnitude of the electric field at a distance
a
above the center of the disc is given by?
An infinitely large surface of uniform charge density
σ
has a disc of radius
R
cut out (see figure). The magnitude of the electric field at a distance
a
above the center of the disc is given by?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Shit man. I by mistake took it a ring. Anyways thanx
Consider elemental ring of radius x and thickness dx on sheet. Using this calculate the net electric field by putting limits R to infinity.
Note : For finding the electric field at a distance x from a charged circular disc of surface charge density σ , one should consider elementary rings of charges on the disc and then integrate.