Find the equilateral triangle 🔺
Given point , lines , find the equilateral triangle with on , on , and with a smaller -coordinate.
If
, find
(because of a slight mistake in the answer :| sorry for the inconvenience)
Bonus:
find the general formulas
for
, with
.
This question is
not
completely original.
PLEASE at least ATTEMPT to solve this problem because I’ve got only one attempt per ten views😅
The answer is 18.289335.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since B has a smaller x -coordinate, it is near the LEFT .
With some logic reasoning, we get that B is not just on line l , but it is also on line m rotated 6 0 ∘ counterclockwise from point A . Think! Why? (Hint: it is on an equilateral triangle, so B rotated 60 degrees clockwise is on m)
This works in the different direction for C , which I will use in my approach.
Now we find that y = 5 rotated 6 0 degrees clockwise from the origin is − 3 + k . Why? (Hint: slope & tangent 60)
Call this line l ’ . Let’s find k .
We know that the distance between l ’ and A is 5 . Construct the line perpendicular to l ’ at P . So A P = 5 . Solve for ( 3 1 n ) 2 + n 2 = 5 . We get n = 2 5 3 .
Now we solve for f ( x ) = − 3 x + k with f ( 2 5 3 ) = 2 . 5 .
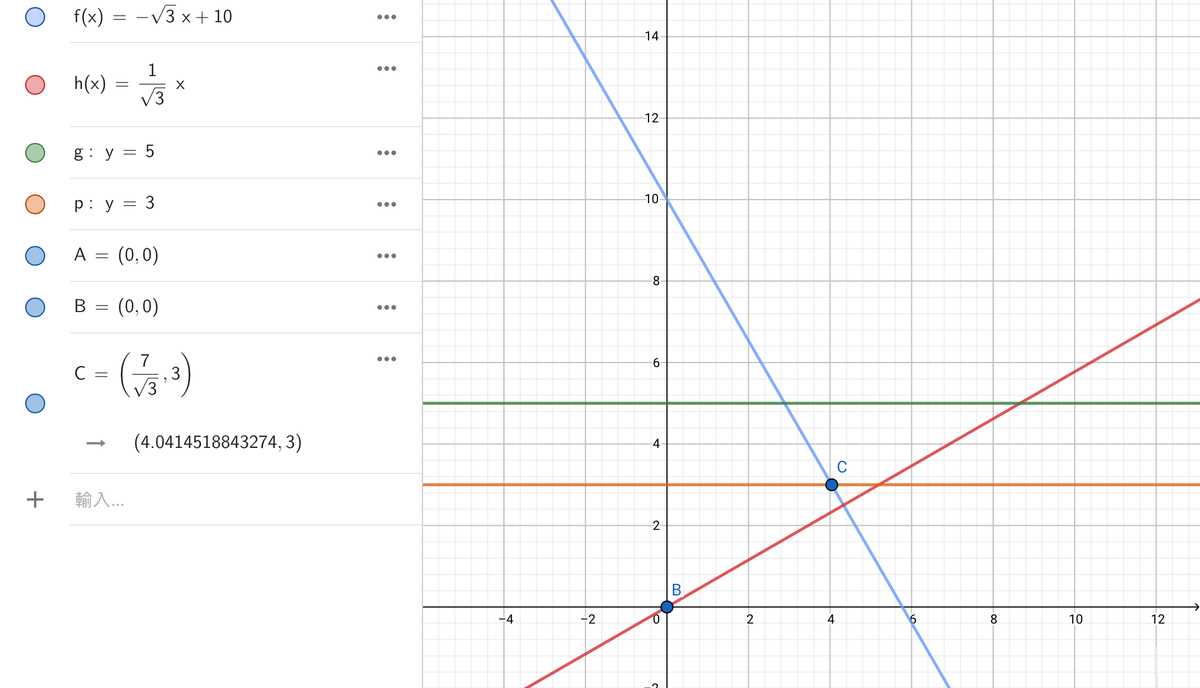 Above pic shows how far we’ve gone now :j (ignore the
B
)
Above pic shows how far we’ve gone now :j (ignore the
B
)
We find k = 1 0 . Now since C is on lines l ’ & m , we can solve for C : − 3 x 2 + 1 0 = 3 − 3 x 2 = − 7 x 2 = 3 7 = 3 7 3 . So C ( 3 7 3 , 3 ) .
Now we solve for B by rotating C 6 0 degrees counterclockwise from A .
We can use a formula , so B ( x 1 , y 1 ) is as follows:
x 1 = 3 7 3 cos 6 0 ∘ − 3 sin 6 0 ∘ ,
y 1 = 3 7 3 sin 6 0 ∘ + 3 cos 6 0 ∘ . So B = B ( − 3 1 , 5 ) .
So the answer is 3 3 2 = 1 8 . 4 7 5 2 . . . 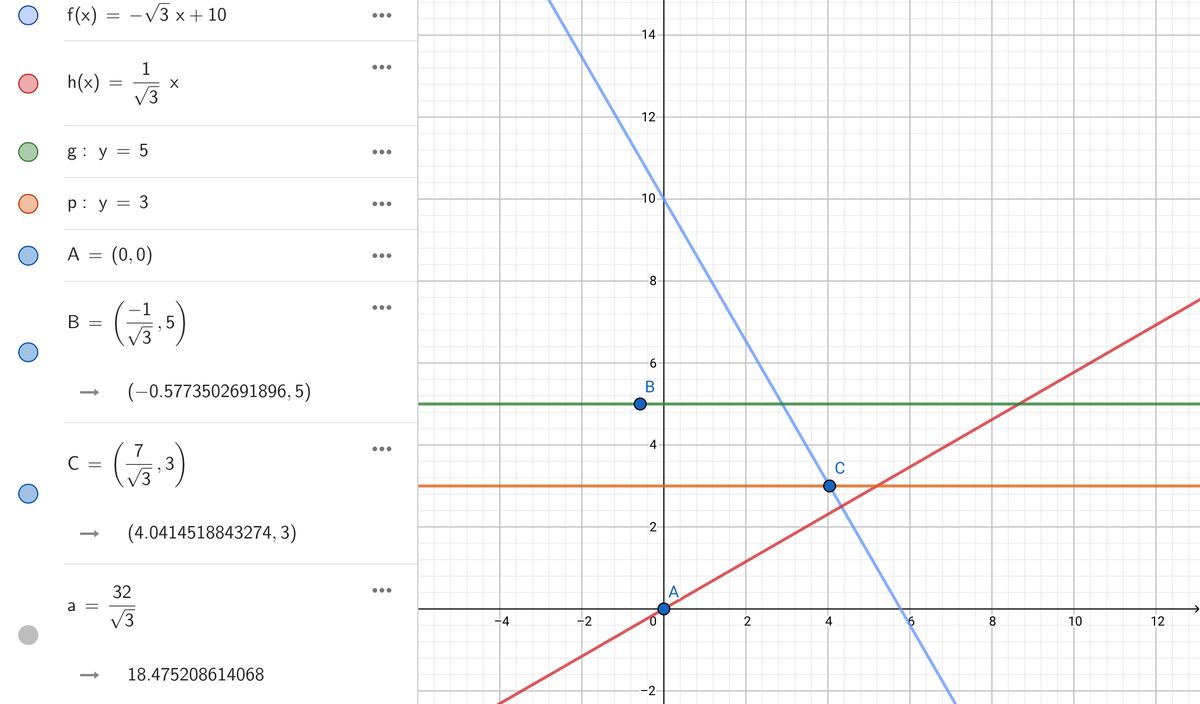
BUT because of my mistake, the answer is 1 8 . 2 8 9 3 3 5 so please subtract the value stated in the question :P