Find the Expected Area

Calculus Level 3

A unit circle is constructed centered at ( 0 , 0 ) (0,0) . A point A A is uniformly and randomly chosen on the circumference of the circle with the constraint that point A A is in the first quadrant.

A rectangle is then drawn with one vertex at A A and the vertex opposite A A at the origin ( 0 , 0 ) (0,0) , as shown in the following image:

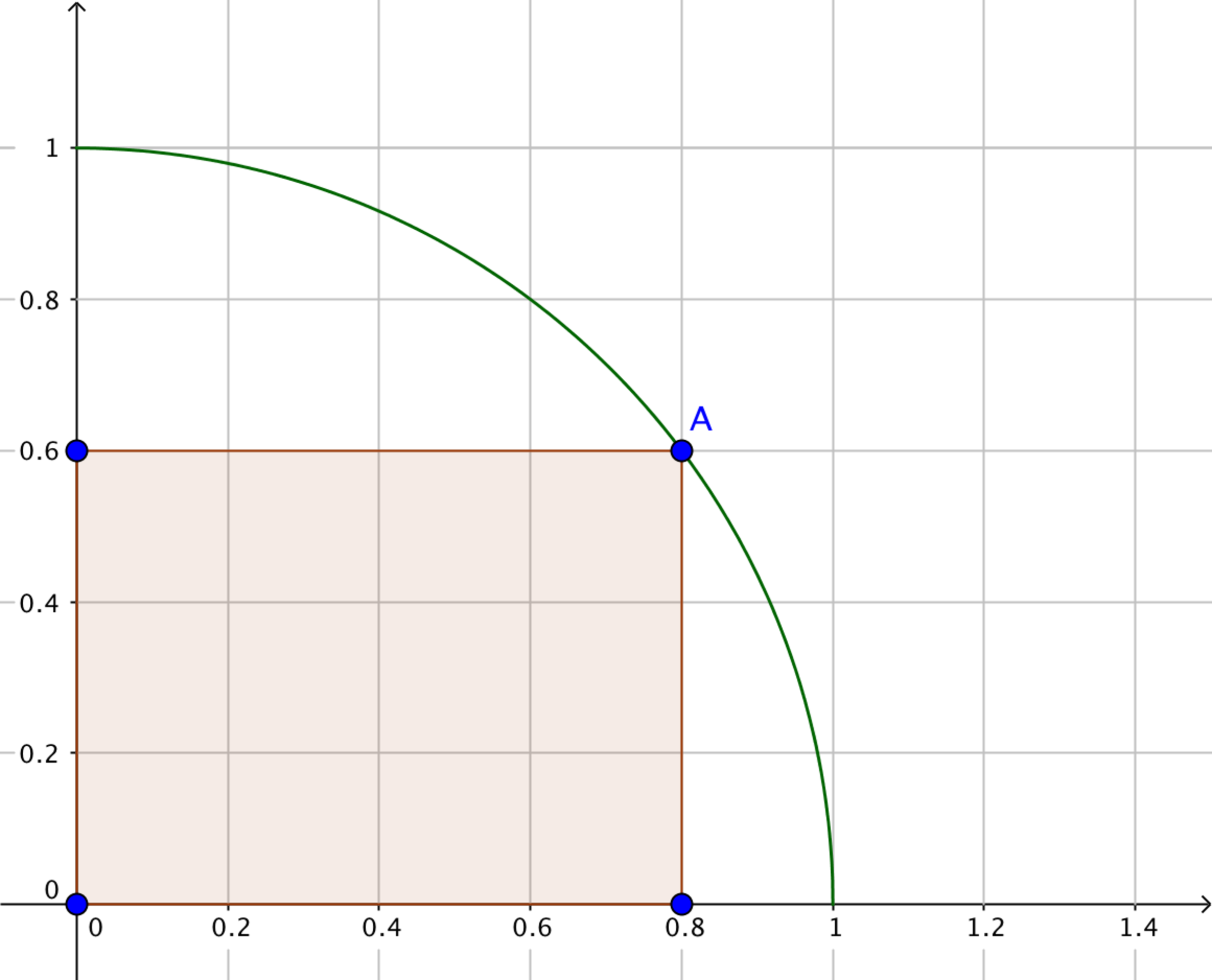
What is the expected area of the rectangle?

1 3 \frac{1}{3} 1 π \frac{1}{\pi} 2 4 \frac{\sqrt{2}}{4} 1 2 ln ⁡ 2 \frac{1}{2}\ln{2} π 10 \frac{\pi}{10} 1 2 \frac{1}{2} 1 e \frac{1}{e} 1 4 \frac{1}{4}

Nick Turtle by Nick Turtle , 21, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Nick Turtle
Dec 10, 2017

To select a point uniformly on the unit quarter circle, it is easiest to select an angle θ \theta between 0 0 and π 2 \frac{\pi}{2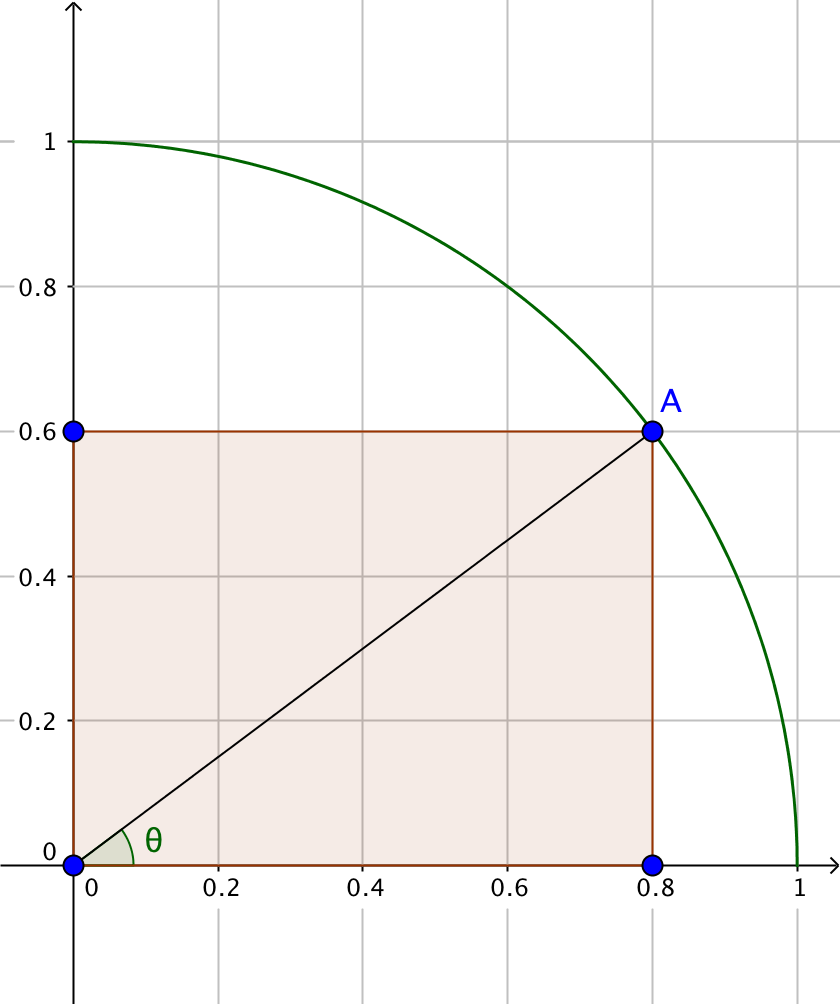} like this:

Then, the height and width of the rectangle is sin ⁡ θ \sin{\theta} and cos ⁡ θ \cos{\theta} , respectively.

Thus, the expected area of the rectangle is 1 π 2 − 0 ∫ 0 π 2 sin ⁡ θ cos ⁡ θ d θ \frac{1}{\frac{\pi}{2}-0}\int_0^{\frac{\pi}{2}}\sin{\theta}\cos{\theta}\ d\theta = 1 π 2 [ 1 2 sin ⁡ 2 θ ] 0 π 2 =\frac{1}{\frac{\pi}{2}}\left[\frac{1}{2}\sin^2{\theta}\right]_0^{\frac{\pi}{2}} = 2 π ⋅ 1 2 =\frac{2}{\pi}\cdot\frac{1}{2} = 1 π =\frac{1}{\pi}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...