Find the Fake!

Suppose there were 27 coins.

We can split them into 3 groups of 9.

We weigh two groups of 9 with each other.

If they are equal, split the last group of 9 into 3 groups of 3, ...

We can easily keep splitting them in groups of 3 until we have found the coin.

This takes $n$ weighings, such that $3^{n}$ is the number of coins.

Now lets go to 25 coins.

We can divide the 25 coins into 2 groups of 9 coins, and 1 group of 7.

Measure the 2 groups of 9 against each other.

If equal, go to a).

If not, go to b)

a) split last group of 7 into 2 groups of 3, and 1 group of 1, and weigh the two groups of 3 together. If equal, the last coin remaining is fake, and if different, take the fake group of 3, and weigh two coins against each other.

b) split 9 into 3, 3 and 3. Weigh two groups of 3 together. If equal, take last group of 3, and if different, take lighter group of 3. With the group of 3, measure two of the coins against each other.

We can say that if $k$ is the number of coins, the number of weighings it takes is n, such that $3^{n-1}$ < k < or equal to $3^{n}$

[Weigh 1] You divide 27 coins to 3 groups, each group consists of 9 coins. There are group A, B and C. You weigh group A and B. If they balance, group C has the fake coin. If not, you know which has the fake coin.

[Weigh 2] Let's take the group with the fake coin. You divide it to 3 groups of 3. Group A, B and C. You weigh group A and B. If they balance, group C has the fake coin. If not, you know which has the fake coin.

[Weigh 3] You can repeat the steps above

*pardon my english

I believe this question evolved from the original one which would only involves 8-9 coins. Nevertheless, the answers follow the same pattern: You'd divide the coins into a number of groups so that 1 weight immediately derives the group that has the fake coin. The answer is 3 groups: weight 2 groups and left out 1 group. If 2 weighted groups are balance, the left-out one is the one, otherwise whichever lighter group on the scale.

Applying that to this question: 25 = 8/8/9 -> 9 (worst case we have 9) = 3/3/3 -> 3 = 1/1/1. Answer: 3 times.

Weigh 12 coins in each pan if they balance, you have the light coin in your hand. I agree, that the chances of having only heavy coins in this first weighing are very slim, there is a chance that one weighing could determine which coin is the light one

Please write these problems correctly The phrase "" the fewest weighings you can make."" means what is the least amount of weighings possible """.

Now, It is certainly possible for me to choose a coin at random and separate it from the rest.
Then I split the remaining 24 into 2 groups of 12.
It is certainly possible that both groups weigh the same. Which would mean that I have the lighter coin in my hand.
This means that the least amount of weighings possible is 1 !!! Not 3 !!!

I had to choose the "" try again """option just to write this correction.. Which was totally uncalled for. !!

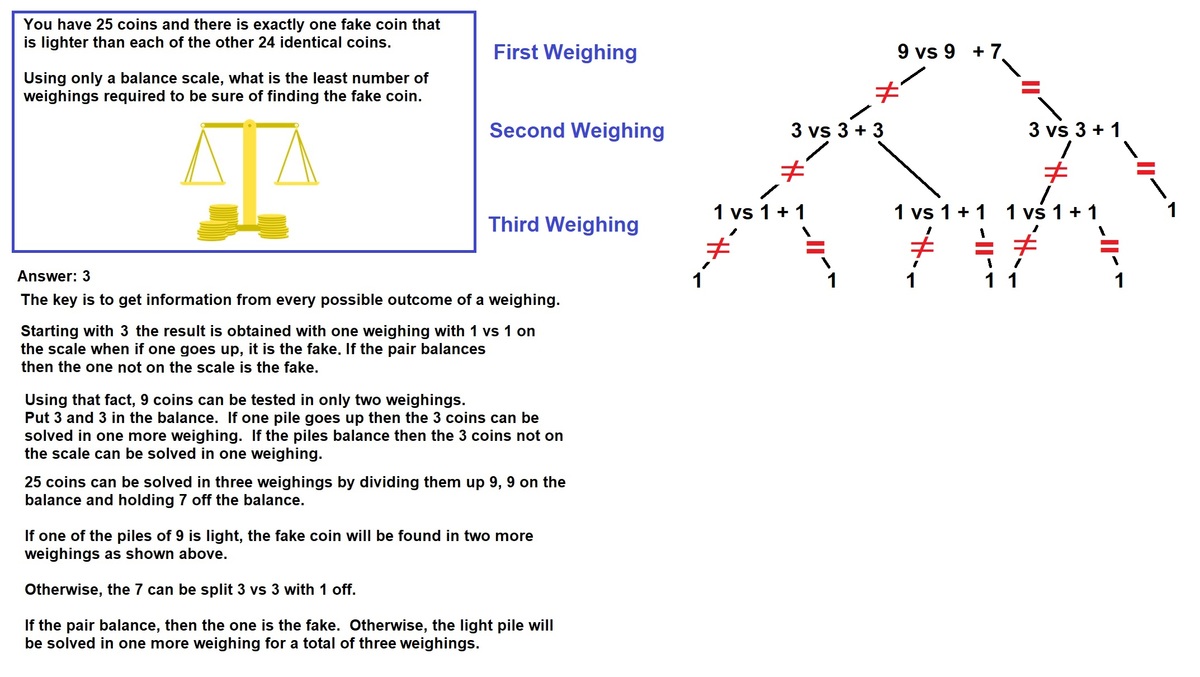
It is convenient to split the number of coins in 3 because in that way you can also use the information coming from the fact that the two plates of the scales are in balance. Of course, on each plate must go the same number of coins.

In our case, with 25 coins:

1st weighing) Divide 25 in three groups of 9, 8 and 8 and put on the plates the two groups of 8. If the plates are balanced then the fake coin is in the group of 9, otherwise it is in the lighter group of 8.

2nd weighing - 9 coins) If the fake coin is in the group of 9, divide this in 3 groups of 3 and weigh two of them. Again, if the plates are balanced then the fake coin is in the group left out, otherwise it is in the lighter of the two which have been weighed.

2nd weighing - 8 coins) If the fake coin is in the group of 8, divide this in one group of 2 and two of 3 and weigh these. If the plates are balanced then the fake coin is in the group of 2, otherwise it is in the lighter of the two groups of 3.

3rd weighing - 3 coins) When you have a group of 3 coins, weigh two of them. Then, if the plates are balanced the fake coin is the one left out otherwise is the lighter one of the two which have been weighed.

3rd weighing - 2 coins) When you are left with 2 coins just weigh them and determine the lighter one.

Therefore, we just need $\boxed{3}$ measures.

I got two weighings. Someone correct my logic if I'm wrong.

I'm working on the assumption I got lucky and found the coin, or I already know the coin is lighter and I want to confirm.

Separate the coins into five groups of five coins. AAAAa BBBBB CCCCC DDDDD EEEEE. Select the A and B group and weigh them. (AAAAa) <> (BBBBB), and find the A group is lighter. Discard B group. Remove the 'a' coin from the A group and weigh two groups of two coins (AA) <> (AA), and find they're equal. The 'a' coin left out is lighter.

Take aside one coin. Weight two groups of 12. If they weigh the same, then the one you took aside was the fake. So one measurement is the minimum that would ensure that you had found the fake.

Answer:3 Since total number of coins (25) is less then or equal to 3 power number of times (3). ie. 25<=3^3.

In every weight there are 3 possible outcomes: balanced, left, right. This is the information we can get from each experience.

The problem is similar to binary search where one successively divides an interval in half until the correct result is found. In our case we divide it in 3.

On average we need $\log_3(25)\approx2.9299$ weightings, and can guarantee a maximum of 3 weightings.

Picking a small nit regarding the wording in the problem: "fewest weighings... to ensure that you can determine the fake coin?"

I'd say the answer to that question is zero. I can state with certainty, without actually performing any weighings, that I could determine the fake coin by performing weighings if I wanted to.

Removing "ensure that you can" would more clearly indicate what the puzzle intends me to work out.

Creo que en el mejor caso bastaría pesar una sola vez. 12 y 12, y suponer que la falsa queda afuera.

While I got this correct on the first attempt, the truth is a person could get really lucky and find the lighter coin with only a single weighing. Seeing as this had 25 coins, one could put 12 on each side of the scale, if the scale balanced then the one coin that was not on the scale would have been the light one. However, if it did not balance then it would take the 3 tries that was the answer to this question, as you would have to split the lighter stack on each side of the scale as you progressively reduced the possibilities until you had 3 coins, which again on the third attempt if the scale balanced the one left out would be the lightest, if not then it would be obvious which side of the scale the lighter coin was placed on.

W/g mnie te 3 wazenia to za dużo. Wystarczy jedno wazenie.Ale niech Wam będzie że 3.

I think 1 try is pretty possible