Find The Frog!

Let an $\text{O}$ denote where the biologist checks, and let an $\text{X}$ denote a pond where the frog cannot be. In order to devise a strategy that will guarantee that she eventually discovers the frog, we will always assume the worst case. That is, she will never discover the frog in a pond until the frog must be in that pond.

At the beginning, the biologist has no idea where the frog is. The first day, she checks the inner-left pond (and doesn't find the frog).

$\underline{\hphantom{O}} \ \underline{\text{O}} \ \underline{\hphantom{O}} \ \underline{\hphantom{O}}$

She doesn't know where the frog is among the remaining 3 ponds. Now she checks the inner-right pond the next day (and doesn't find the frog).

$\underline{\text{X}} \ \underline{\hphantom{O}} \ \underline{\text{O}} \ \underline{\hphantom{O}}$

The frog cannot be in the leftmost pond (it wasn't in the inner-left pond the previous day). She checks the same inner-right pond again (and doesn't find the frog).

$\underline{\hphantom{O}} \ \underline{\text{X}} \ \underline{\text{O}} \ \underline{\text{X}}$

Now she knows that the frog cannot be in the inner left pond (it wasn't in the leftmost pond or the inner right pond the day before), and she also knows that it isn't in the rightmost pond (it wasn't in the inner-right pond the day before). The frog is in the leftmost pond! Unfortunately, she can't check until the next day. She knows the frog will move to the inner-left pond, so that's where she checks.

$\underline{\text{X}} \ \underline{\color{#20A900}\text{O}} \ \underline{\text{X}} \ \underline{\text{X}}$

And she finds the frog!

Addendum: Of course, the biologist could always get lucky and discover the frog before this day, but this strategy ensures that she discovers the frog on the fourth day even in the worst case.

The lazy solution would be to check the same pond every day until the frog eventually arrives there .

The information doesn't mention any thing regarding whether the frog travels linearly from one pond to the next nearest pond or whether it has the option to move randomly from pond to pond. I'm assuming the former and suggest that she visits the same pond each night until the frog passes by. She might get lucky and see the frog on the first night but ina any case will have to wait no longer than 4 nights if she chooses the second or third pond.

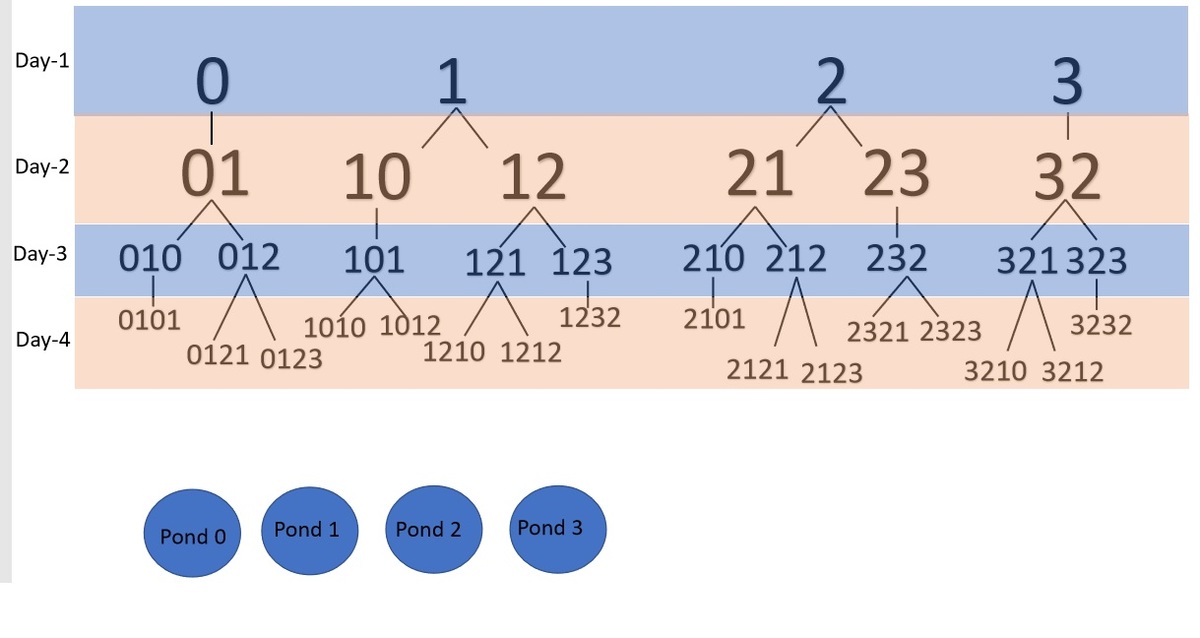
The tree structure represents all possible pond location histories after day-1, day-2, day-3 and day-4. We can see that there is a total of 16 possible day-4 sequences. The last digit corresponds to where the frog is on day-4 and the first 3 digits to the frog’s history (see the bottom layer on the tree structure). Choosing pond 1 or pond 2 on day-1 will eliminate 5 day-4 sequences. For example, just by choosing pond 1 and missing, we can reduce day-4 to 11 possible sequences: 0101, 0121, 0123, 2101,2121,2123,2321,2323,3210,3212,3232. Right away we can see only 1 of these sequences end in pond 0, 2 of these sequences end with the frog in pond 2, 5 sequences end with the frog in pond 1, 3 sequences with the frog in pond 3. We can eliminate the possibility of pond 0 and pond 2 from being the day 4 location, simply by checking pond 3 on day-2. This leaves us with 8 possible day-4 sequences: 0101,0121,0123,2101,2121,2123,2321,2323. The day 4 sequences ending in pond 3 can be eliminated by checking pond 2 on day 3, thus leaving pond 1 as the only possibility. Follow the tree structure trail to correspond to the nice solution that Andy Hayes posted.

Number the ponds 1 through 4. We will prove that checking ponds 2, 3, 3, and then 2 suffices.

Note that the frog alternates between being in even-numbered and odd-numbered ponds each day.

Say the frog starts in an even pond. The second day it will be in an odd pond. The only way the frog can evade detection is by being in pond 4 the first day (he's in an even pond and we checked 2), and pond 1 the second day. This is impossible, so he will be caught.

If the frog starts in an odd pond, then on the third day it will be in an odd pond and on the fourth day it will be in an even pond. The only way the frog can evade detection is by being in pond 1 the third day (he's in an odd pond and we checked 3), and pond 4 the fourth day. This is impossible, so he will be caught.

Response to Challenge Master's Extension:

STRATEGY visit each consecutive pond for 2 starting from the second until the second last. Then starting from the third last, stay 1 day for each pond until you reach the second from the beginning, then stay in each pond for 1 day starting from the second (the second would have been stayed for two) until you reach the second last again:

(number after the semicolon stands for the pond i.e. 2 is the second pond; slash stands for a change in direction) 4 ponds: 2233/2 5 ponds: 223344/32/23 6 ponds: 22334455/432/234 7 ponds: 2233445566/5432/2345 etc

The reason why this works is because in the first direction (staying 2 days each), you let the possibility of the frog crossing (switching spaces with) you only on EVERY OTHER day. Thus limiting the frogs possible position in the ponds you passed. Then when you switch direction, you only let every other frog pass you, and corner every other frog. And the last time, because the frogs are only on every other pond, you will corner and find all the possible route of the frog.

A better way to explain this and also the means by which i came to this solution is by geometry: (across the top is the pond, down the side is the day, "X" is where the biologist is, the dot is where the frog can possibly be)

I can check the second pond for the first time so the frog can either be 1, 3 or 4. Next day I check pond 2 again to if the frog isn't here means that the frog cannot be in Pond 1 therefore it must be at pond 3 or 4.

Next day I check the pond 2 again, if frog is not there it means the frog was in Pond 3 now moving to Pond 4 or the frog was in Pond 4 now moving is in Pond 3.

Finally I check Pond 3, if the frog is not here mean the frog is in Pond 4. So I simply check Pond 3 and the frog would be there.

If I were the biologist I would visit the two inner ponds alternately as the fastest method of finding the frog since visiting the outer ponds has less chance of seeing the frog. Visiting the outer ponds, the frog could be alternating between the other three and never visiting that pond. Therefore eliminating the outer ponds the frog must be seen in an inner pond eventually. The frog can't possibly cross the inner ponds without being spotted and it cannot remain in an outer pond indefinitely.

Generalisation to $n$ ponds:

• Number the ponds from $1$ to $n$ .
• First, check ponds $2$ to $n-1$ in order.
• Then, check ponds $n-1$ to $2$ in order.

This gives a worst case of $2n-2$ days to find the frog.

Why it works

First, note that each night the frog will jump from an odd-numbered pond to an even-numbered pond or vice versa.

Suppose the frog started in an even-numbered pond. Then if the first check doesn't find the frog, then the frog must be in one of the even ponds $\geq 4$ . Therefore, on the first night the frog will jump to an odd pond $\geq 3$ . Then we will check pond 3, and the process will continue. Note that the number of the frog's actual pond will always have the same parity as that of the pond we're searching on a given day. So when we reach pond $n-1$ , the frog cannot be in pond $n$ since it has the wrong parity, and therefore must be in pond $n-1$ . We've found the frog!

Suppose the frog started in an odd-numbered pond. Then the checks from ponds $2$ to $n-1$ won't find the frog. At this point, $n-2$ checks have been made, therefore the following day the frog will have jumped $n-2$ times. So for odd $n$ , the frog will now be in an even-numbered pond; for even $n$ , the frog will now be in an odd-numbered pond. And so searching pond $n-1$ again has the possibility of finding the frog. Otherwise, we apply the same argument as before, going in the opposite direction.

Visualisation of the solution for $n = 10$ : Ponds are from left to right; successive days are from top to bottom. Blue denotes the pond we're checking, and green denotes the other possible ponds the frog might be in.

My initial instinctive solution is this one:

Naming the ponds 1, 2, 3 and 4 from left to right.

The biologist checks pond 2 for two days in a row, then checks pond 3 for two days in a row.

This way it would take maximum four days for the biologist to find the frog.

Please comment with your thoughts on my solution :-)

lets start with four possible frog locations labeled A,B,C and D. Start with the four potential frog locations in the four ponds ordered A.B.C.D

• On the first day check the inner left pond, if no frog than you can eliminate B. so you have A.-.C.D
• At night the frogs jump to a random neighbor pond creating possibilities -.A.D.C or -.A.-.C or -.D.-.C
• On the second day check the inner left pond again, if no frog you have eliminated A and the possibility where D jumped into the inner left, on the second night the frog jumps and the possibilities are now -.-.C.D or -.D.C.- or -.-.C.-
• Third day check inner right and you have eliminated possible frog C, third night the frogs move and you have -.-.D.- or D.-.-.-
• Fourth day check inner right, if no frog than wait a night and the frog will be at the inner left pond on the fifth day.

Let's say there are $N$ ponds. We will show that there exists a strategy that finds the frog by night $N$ . The probabilistic method will be used, so the existence of the strategy will be proven, but the strategy will not be given explicitly. Our randomized strategy is as follows: on each night choose a pond uniformly at random from $1$ to $N$ . Do this for $N$ nights regardless if we find the frog early on or not. Let $X$ be the number of times we find the frog (note that this is a random variable). Let $X_i$ indicate whether or not we found the frog on night $i$ , i.e. $X_i = 1$ if we found the frog on night $i$ and 0 otherwise. Then $X = X_1 + X_2 + \ldots + X_N$ . By linearity of expectation, the expected number of times we find the frog is then $E[X] = E[X_1] + E[X_2] + \ldots E[X_N]$ . For each $i$ , we have that $E[X_i] = P(X_i = 1) = \frac{1}{N}$ since we choose a pond uniformly at random. Therefore, the expected number of times we find the frog is $E[X] = N \times \frac{1}{N} = 1$ . Since $E[X] = 1$ , there must be a sequence of N ponds $\omega$ (i.e., a strategy) such that $X(\omega) \geq E[X] = 1$ .

This may not be the most elegant proof, but I'm a sucker for the probabilistic method :)

Check the same pond!It says that the frog hangs out in the pond in the day. So check the same pond everyday. Easy peasy!

Yes! I remember hearing of this problem when I was like 10, except it was a princess and a castle with 4 doors, and you couldn't pick the same door in two consecutive days.

If you removed that last rule, you could do it in 4 days, with that rule, it took you 5.

I remember even generalizing a solution!

Basically, the key is to think of it as if the frog starts in all of the ponds simultaneously, you can think of them as being "lit up", and when you check one, you turn it off. Every day, all ponds are lit up only if they have one adjacent pond lit up. If you find a strategy to make sure they're all turned off, you win, because it means you checked every possible move the frog could've made.

Something to note is that the parity of the position of the frog changes every day: if one day it's on an even pond, the next day it must move to an uneven one. This basically divides the problem into two equal parts: the one where the frog starts on an even position, and the one where it starts on an uneven one. With this, if you manage to solve one of these parts, you'll for sure be able to solve the other one.

To solve any of these parts: check in a pond that's adjacent to a corner, this will make it so that in the next turn, when the parity changes, the frog can be in any place of that same parity, except the corner one that you checked. Now choose the third pond from the corner (that is lit up not because it was adjacent to the previous second from the corner, because you turned that one off, but because it was adjacent to the fourth from the corner) and keep going like this, working your way to the other side, until you get completely rid of that parity group. Now repeat for the other one.

check each pond twice: let's say the frog is in the 4th pond and the biologist started to check ponds at the first one today. İf the biologist checks the first pond tomorrow and then go for the second and checks it in the following day and so on...even the frog moves from #4 to #3 then #3 to #4 everyday or moves like 4-3-2-1 it will be found in the end.

She needs to start from one side, if she got lucky great. If not, she need to visit it again. If she got lucky great. If not she need to visit the nearest pond, which she will need to visit one more time. Than again, If she got lucky great. If not she need to visit the nearest pond, which she will need to visit one more time. Eventually she will get across the rare frog.

Assigning numbers 1 to 4 to the four ponds, from left to right, 1 - 2 - 2 - 3 - 3 - 2 will ensure finding the frog.

She can stay at same pond until the frog come there

If she checks the number 2 pond everyday, she'll find the frog in 3 days in worst case.

My thinking is that the biologist could stay in 1 pond for 4 days and eventually the frog would come

Label Ponds 1 to 4 left to right. Check pond 2. If frog not found then the next night check pond 3. No frog? Then he is in either 2 or 4. He either moved from 1or 3 to 2, or he moved from 3 to 4. Check 3 again. No frog? He was in 2 is now in 1 will be in 2 again tomorrow.

1,2,2,3,3,2.

I have a question (An sorry if it contains flawed logic please englighten me): I am stronlgy the opinion that the stated conditions are missing an important information. To my idea I cannot create a strategy because it remains unclear if the overlap between moving at night an checking during daytime creats an oberservation blind spot. Meaning: when she can only check 1 pond during daytime an the result is false but the frogs moves during night to exatly the spot she is waiting. Will she have to spend another check on the pond she is already sitting on or would this be an automatic win? If this is NOT the case then to my thinking it is impossible by logic to find the frog because there is a chance that she is always missing it because the frog could move just random jump between the positions during night, while she was always having "bad luck" doing the check. So she has to pick random positions. Eventually on every iterations here chances to get lucky increases but because of the missing options to doublecheck there is no strategy. Please correct me! Thanks Tim

I found a winning solution to be: 4 - 2 - 2 - 3 - 3 - 2. This combination will always find the frog.

Just check the first pond in the morning and the fourth in the night... If the frog isnt in the first at morning ans not in the fourth at night, he must ne in the third at night.

A full proof solution would be to check pond 2 twice, then pond 3 twice, then check pond 2 again. It may not be the quickest solution, but it is simple. I will explain each check and what it establishes assuming the frog is not caught in the check.

• Check pond 2
  • The frog did not start in pond 2.
• Check pond 2 again
  • The frog did not start in pond 1 since it would've had to move 1->2.
• Check pond 3
  • The frog did not start in pond 3 because it made 2 moves so far and if it was 3->2 it would've been found during the 2nd check. So its 3 moves would have had to be 3->4->3. And since it is not found, The frog had to start in pond 4.
• Check pond 3 again
  • Checking pond 3 again ensures that the frogs path could not be 4->3->4->3 and it could not be 4->3->2->3. So, the only possibility left is 4->3->2->1. And so after this check it has to move back to 2. So checking pond 2 again will find the frog.

We will first check the last pond on the right, Hence there is probability of 1/4 for finding the frog there and 3/4 for not finding it. Now if we don't find it there then it must have been somewhere in the other three ponds. Now we check in the second pond from left . If we do not find the frog there then it is obvious that it has gone to the last pond on the right as if it would be/go in the neighbouring ponds then it would get caught . Hence it is necessarily in the last pond on the right . Answer in two steps.

I suppose that the biologist come to check during the day, so no way to see the frog during the night, I.E. seeing the frog during the change. I found a solution in maximum 5 days. If the biologist check the 2nd pond the first 2 days, he or she will find the frog if located in pond 1 or 2 the first day. Obviously the first day if frog starts in pond 2, the second day if frog starts in pond 1, as the frog has to move from pond 1 to pond 2 the first night. If frog has not been found at the end of day 2, that's mean frog was in pond 3 or 4 the first day.

If the frog starts in pond 3, it moves to pond 2 or 4 the second day. If it selects pond 2 it will be find by biologist the day 2. If move to pond 4, it will be back in pond 3 the day 3 where the bilogist has to stay this day 3.

Worst case is if frog start in pond 4, as when biologist change from pond 2 to 3 the 3rd day, frog could be located now on the left side. A short tree case will be easier to explain: 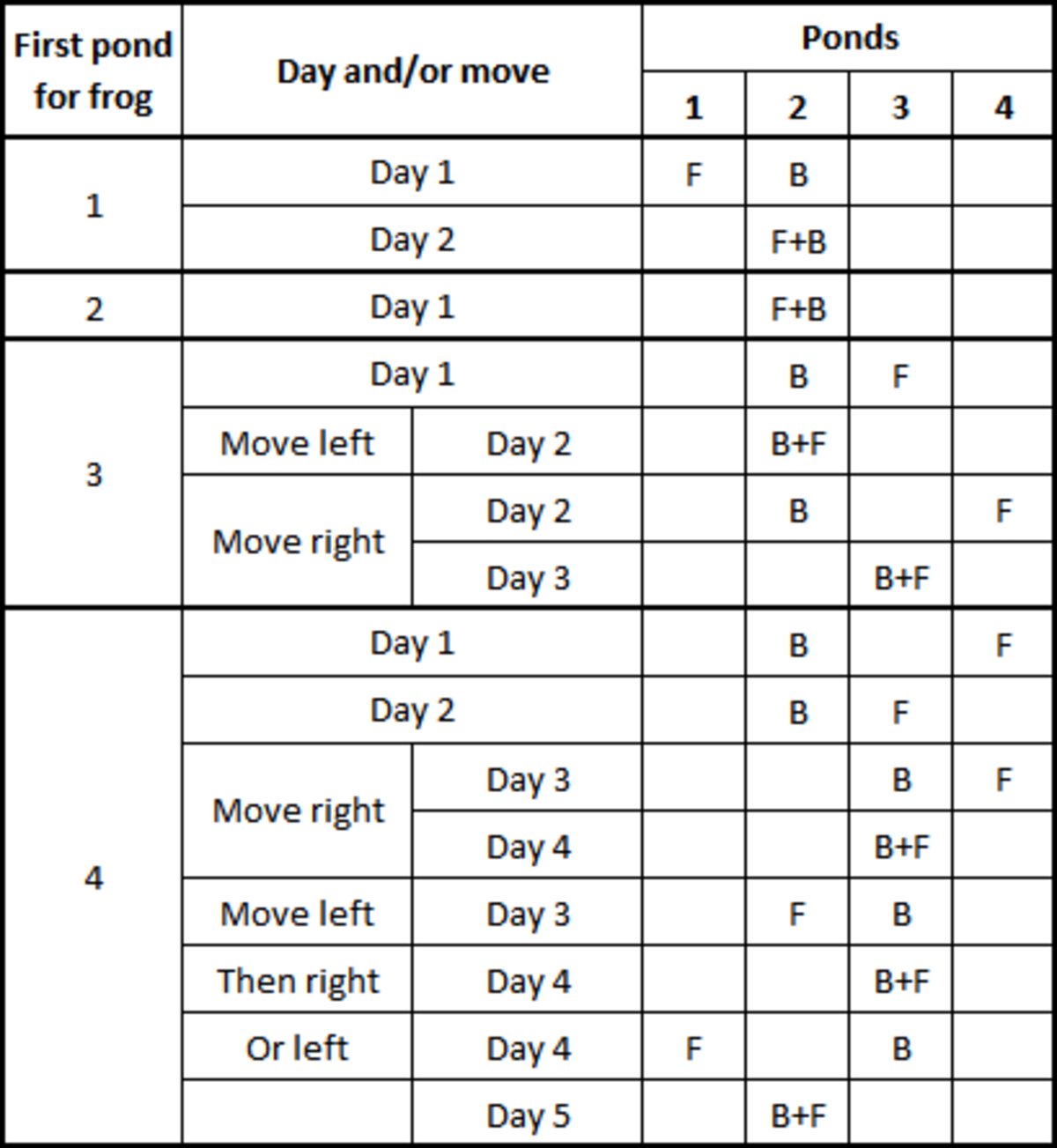In a conclusion, biologist has to stay in pond 2 the first 2 days ,then check pond 3 for day 3 and 4 and back to pond 2 the 5th day if not found before.

Start by checking the left center twice in a row, then the right center twice in a row, then back to left center. You will have caught the frog somewhere in that sequence. Try it and see.....

If we need just a stratagy (not necessary optimal). It's easy. Let's first idealize. If frog trajectory goes through all ponds, check the same pond for a long time (possibly infinitelly long) till you find the frog. If frog moves randomly (all available directions are equally likely), we can check one of the two central locations as they are more likely. Now, let's make it worse for this strategy. The frog can be jumping between neighbouring ponds, let's say 3 and 4. If we are checking pond 2, we will never find it. Listing all possibilities: the frog can be looping between 1 and 2, 2 and 3, 3 and 4. In all cases, it should be present from time to time in either 2 or 3 (central locations). So we can check randomly either 2 or 3 till we find it. We are done.