Find the height of the trapezoid

If $h$ is the height, set coordinates as $A(4,h), B(0,0), C(12,0), D(8,h)$ . Since $AC\perp BD$ , the vectors $(8,-h)$ and $(8,h)$ are perpedicular, so their inner product $64 - h^2$ is $0$ . As $h > 0$ this implies $\boxed{h = 8}$ .

Draw $EM \perp AD$ and $FM \perp BC$ .

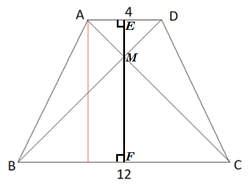
Then $\triangle MEA \cong \triangle MED$ by HL congruence, and $\angle AME = \angle DME = 45°$ , so $\triangle MEA$ is an isosceles right triangle so that $EM = AE = 2$ .

Similarly, $\triangle MFB \cong \triangle MFC$ by HL congruence, and $\angle BMF = \angle CMF = 45°$ , so $\triangle MFB$ is an isosceles right triangle so that $FM = BF = 6$ .

Therefore, the height of the trapezoid is $EM + FM = 2 + 6 = \boxed{8}$ .

Let the intersection of AC and BD be M, and the foot of the perpendicular on BC be N. Then since $\angle AMD = \angle BMC = 90º$ , by Pythagoras $BM^2 + CM^2 = 12^2$ , and since the trapezoid is isosceles, $BM = CM$ . Therefore, $2 BM^2 = 12^2 \Rightarrow BM = 6 \sqrt{2}$ . Similarly, $AM = 2 \sqrt{2}$ .

Since $AMB$ is a right angle as well, $AB^2 = (2 \sqrt{2})^2 + (6 \sqrt{2})^2 = 80$ . Therefore $BN^2 + AN^2 = AB^2$ and $BN = \frac{1}{2}(12 - 4) = 4$ , so the red line $AN = \sqrt{80 - 4^2} = 8$ .