Find the Inductance
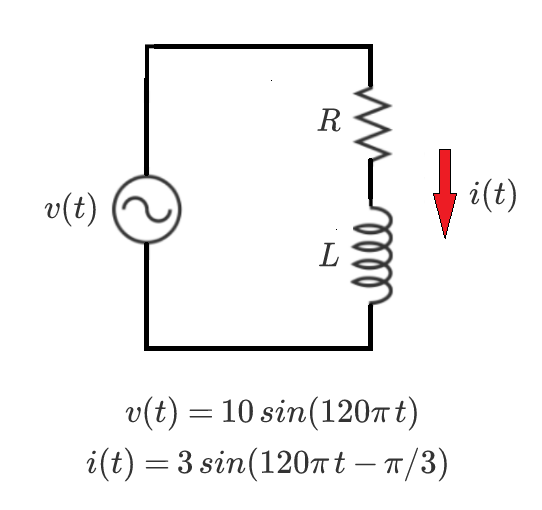
An AC voltage source drives a series R L circuit. Given the voltage and current expressions, determine the value of the inductance L in milli-Henries ( m H ) .
The answer is 7.657.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The impedance of the circuit is given by:
Z ⟹ R + j ω L R + j 1 2 0 π L ⟹ 1 2 0 π L L = i ( t ) v ( t ) = 3 ∠ ( − 3 π ) 1 0 ∠ 0 = 3 ( 2 1 − j 2 3 ) 1 0 = 3 1 0 ( 2 1 + j 2 3 ) = 3 5 ( 1 + j 3 ) = 3 5 = 3 × 1 2 0 π 5 ≈ 7 . 6 5 7 mH where ω = 1 2 0 π Multiply by 2 1 + j 2 3 2 1 + j 2 3 Equating the imaginary parts
@Steven Chase , just like other functions such as \ln ln , \log lo g , \int ∫ , and \sum ∑ , we should have a backslash before \sin sin , \cos cos , \tan tan and other functions. Note that the sin in \sin x sin x is not in italic which is for variable and constant such as x. Also note that there is a space between sin and x while sin x s i n x has no space and all letters are in italic.
Another solution exploits Kirchhoff's Voltage Law for this series RL circuit:
v ( t ) = R i ( t ) + L i ′ ( t ) ;
or 1 0 s i n ( 1 2 0 π t ) = R [ 3 s i n ( 1 2 0 π t − 3 π ) ] + L [ 3 6 0 π c o s ( 1 2 0 π t − 3 π ) ] ;
or 1 0 s i n ( 1 2 0 π t ) = 3 R [ s i n ( 1 2 0 π t ) c o s ( 3 π ) − c o s ( 1 2 0 π t ) s i n ( 3 π ) ] + 3 6 0 π L [ c o s ( 1 2 0 π t ) c o s ( 3 π ) + s i n ( 1 2 0 π t ) s i n ( 3 π ) ] ;
or 1 0 s i n ( 1 2 0 π t ) = 3 R [ s i n ( 1 2 0 π t ) ( 2 1 ) − c o s ( 1 2 0 π t ) ( 2 3 ) ] + 3 6 0 π L [ c o s ( 1 2 0 π t ) ( 2 1 ) + s i n ( 1 2 0 π t ) ( 2 3 ) ] .
By matching coefficients for the sine and the cosine terms, we now obtain the following system of linear equations:
1 0 = 2 3 R + 1 8 0 π 3 L ; (i)
0 = − 2 3 3 R + 1 8 0 π L ; (ii)
which solving R for L in (ii) gives R = 3 1 2 0 π ⋅ L . Substituting this value into (i) ultimately yields L = 2 4 π 3 1 = 7 . 6 5 7 × 1 0 − 3 Henries.
I like this approach. This seems like what a physicist with no special EE training might do. Although I am aware that you have such training, and are just having fun. Thanks
From the expressions given, we see that the voltage leads the current by an angle of φ = 0 − ( − 3 π ) = 3 π . Angle φ is also the argument of the complex impedance formed by the series RL netrwork. Maximum values of v ( t ) and i ( t ) are V m = 1 0 V and I m = 3 A , so the RL impedance magnitude is Z = I m V m = 3 1 0 Ω . The reactance of the inductor can be calculated as X L = Z sin φ = 3 1 0 ∗ 2 3 Ω = 3 5 3 Ω , and from that we can determine the value of inductance: L = ω X L = 3 6 0 π 5 3 H ≈ 7 . 6 5 7 m H
where ω = 1 2 0 π r a d / s is the angular frequency of the voltage, and it is derived from the given expression of v ( t ) .