Find the largest Circle
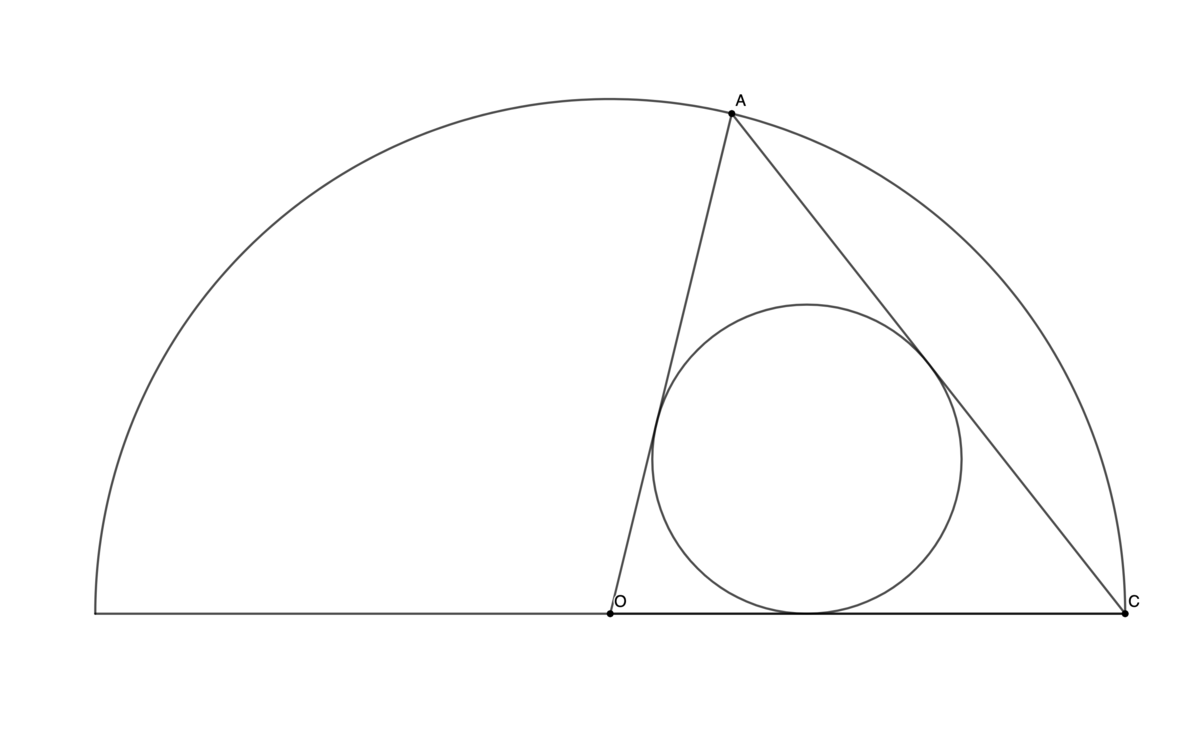
O is the center of this semicircle, A and C lie of the circumference of the semicircle. The length of O A = O C is 1. What is the maximum radius of the incircle of △ A O C ? Express it as c a a − b , where a is square-free and b and c are coprime positive integers. Submit a + b + c .
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let θ = ∡ A O B . The area of the isosceles triangle A B C is A : = 2 1 ⋅ 1 ⋅ 1 ⋅ sin θ = 2 1 sin θ ( 1 )
By cosine rule , the length A C satisfies ( A C ) 2 = 1 2 + 1 2 − 2 ⋅ 1 ⋅ 1 ⋅ cos θ = 2 ( = 2 sin 2 ( 2 θ ) 1 − cos θ ) ⇔ A C = 2 sin ( 2 θ ) ( 2 )
Let the radius of the incircle be denote by r , then A = r ⋅ s , where s is the semiperimeter of the triangle A O C , s = 2 A O + O C + A C = 1 + sin ( 2 θ ) ( 3 )
Thus, we want to maximize r = s A = 2 1 ⋅ 1 + sin 2 θ sin θ , 0 < θ < π ( 4 )
Note that as θ approaches 0 or π , r approaches 0. So one of the critical point(s) of r must be a maximum value.
At its critical point(s), d θ d r = 0 . Applying quotient rule produces 2 [ sin ( 2 θ ) + 1 ] ⋅ = 2 sin 2 ( 2 θ ) cos θ − = 2 sin ( 2 θ ) cos ( 2 θ ) sin θ ⋅ cos ( 2 θ ) = 0
For simplicity sake, let y = sin ( 2 θ ) > 0 , then cos 2 ( 2 θ ) = 1 − y 2 , the equation above becomes 2 ( y + 1 ) ⋅ 2 y 2 − 2 y ⋅ ( 1 − y 2 ) = 0 ⇔ y 3 + 2 y 2 − 1 = 0 ⇔ ( y + 1 ) ( y 2 + y − 1 ) = 0 ⇔ y = 2 − 1 + 5 only
We're left to substitute sin ( 2 θ ) = 2 − 1 + 5 into ( 4 ) .
Rewriting sin θ = 2 sin ( 2 θ ) cos ( 2 θ ) = 2 sin ( 2 θ ) ⋅ 1 − sin 2 ( 2 θ ) ,
we have max ( r ) = 2 5 5 − 1 1 . The answer is a + b + c = 5 + 1 1 + 2 = 1 8 .
Bonus questions :
-
As shown, C is the point of one end of the semicircle. Let B be the other end of the semicircle. Can we find anything interesting about the circle that is inscribed inside the obtuse isosceles triangle O A B ?
-
How do we find the distance between the center of the semicircle and the center of the incircle?
Let the inradius be r and ∠ A C O = θ . Then ∠ A O C = 1 8 0 ∘ − 2 θ and:
r cot 2 ∠ A O C + r cot 2 ∠ A C O r cot ( 9 0 ∘ − θ ) + r cot 2 θ r tan θ + r cot 2 θ 1 − t 2 2 t r + t r t ( 1 − t 2 ) 1 + t 2 r ⟹ r d t d r t 4 + 4 t 2 − 1 ( t 2 + 2 ) 2 t 2 ⟹ t ⟹ max ( r ( t ) ) = O C = 1 = 1 = 1 = 1 = 1 + t 2 t ( 1 − t 2 ) = ( 1 + t 2 ) 2 ( 1 − 3 t 2 ) ( 1 + t 2 ) − 2 t 2 ( 1 − t 2 ) = ( 1 + t 2 ) 1 − 4 t 2 − t 4 = 0 = 5 = 5 − 2 = 5 − 2 = r ( 5 − 2 ) = 5 − 1 5 − 2 ( 3 − 5 ) = 4 5 − 2 ( 2 5 − 2 ) = 2 ( 5 − 2 ) ( 6 − 2 5 ) = 2 5 5 − 1 1 Let t = tan 2 θ To find maximum r Putting d t d r = 0 Since tan 2 θ > 0 As r ≥ 0
Therefore a + b + c = 5 + 1 1 + 2 = 1 8 .