Find the largest prime factor

Consider the factorization $a^4 + 4 = a^4 + 4a^2 + 4 - 4a^2 = (a^2 + 2)^2 - (2a)^2 = (a^2 + 2a + 2)( a^2 - 2a + 2 ).$

Then $5^8 + 2^2 = 5^8 + 4 = (25^2 + 2 \times 25 + 2)(25^2 - 2 \times 25 + 2)$ . The first term is equal to 677, which we can verify is a prime. The second term is less that 677, hence any of its prime factors will be less than 677. Therefore, 677 is the largest prime factor of $5^8 2^2$ .

$N=5^{8}+2^{2}. \ N$ can be expessed as $625^{2}+2^{2}$ . Notice that $gcd(625,2)=1$

According to theorem by Euler all the divisors of $625^{2}+2^{2}$ are of the form $p^{2}+q^{2}$ .

Since $\sqrt{625}=25$ . Let $p=24$ and $q=1$ $\implies$ $24^{2}+1^{2}=577$ , which is prime; but we are going to take $677$ .

To see from where we got $677$ , break down $N$ into two factors in this manner: $5^{8}+2^{2}=((5^{2}+1)^{2}+1)((5^{2}-1)^{2}+1)$ = $677\times577$ $\implies$ the answer is $677$ because it is the largest prime factor.

What I did was write a quick code on Eclipse. It uses a while loop to countdown the numbers i that are divisible by x. If my english makes absolutely no sense, here is an image 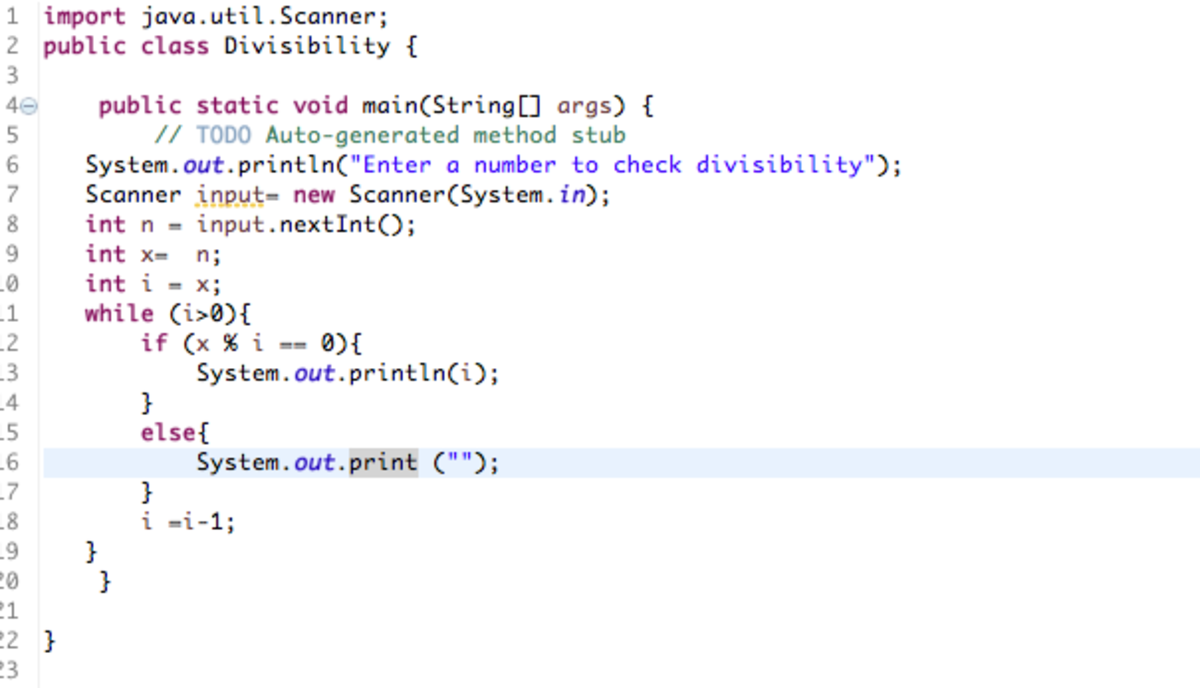there may or may not be some redundancies there.