Find the last digits without the calculator
Without using the calculator, find the last five digits of 5 5 5
Bonus: Show as many ways to solve this as possible.
The answer is 78125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I think nothing new will come out of it.
2 − n = 1 0 n 5 n
So, ultimately you will arrive at the same earlier methods you explained already. :)
For some reason, even though they're the same thing (as you point out), dividing by 2 seems easier than multiplying by 5 .
By Chinese remainder theorem , we have 5 5 5 m o d 5 5 = 0 ; and for 5 5 5 m o d 2 5 , we note that g cd ( 5 , 2 5 ) = 1 , we can apply the Euler's theorem and note that Euler's totient function ϕ ( 2 5 ) = 2 5 × 2 1 = 1 6 . Then
5 5 5 ≡ 5 5 5 m o d ϕ ( 3 2 ) ≡ 5 5 5 m o d 1 6 ≡ 5 7 (mod 32) ≡ 5 ( 1 2 5 ) ( 1 2 5 ) ≡ 5 ( − 3 ) ( − 3 ) ≡ 4 5 ≡ 1 3 (mod 32)
⟹ 5 5 5 ⟹ 3 2 n + 1 3 ⟹ n ⟹ 5 5 5 ≡ 3 2 n + 1 3 ≡ 0 (mod 3125) ≡ 2 4 4 1 ≡ 3 2 ( 2 4 4 1 ) + 1 3 ≡ 7 8 1 2 5 (mod 100000) where n is an integer. Note that 5 5 = 3 1 2 5
On other ways of solving this problem , of course the easiest "way" to solve this is to hit "5^55 mod 100000" in WolframAlpha . Of course, you would said it is numerical method. But in fact is solving 3 2 n + 1 3 ≡ 0 (mod 3125) , I have resorted to Python to solve n = 2 4 4 1 , the other solutions are n = 5 5 6 6 , 8 6 9 1 . Also I think the pattern spotting method proposed by @Chris Lewis would also need a computer to generate the patterns. I just used the Coding environment of Brilliant to get the following pattern. It has a period of 8 .
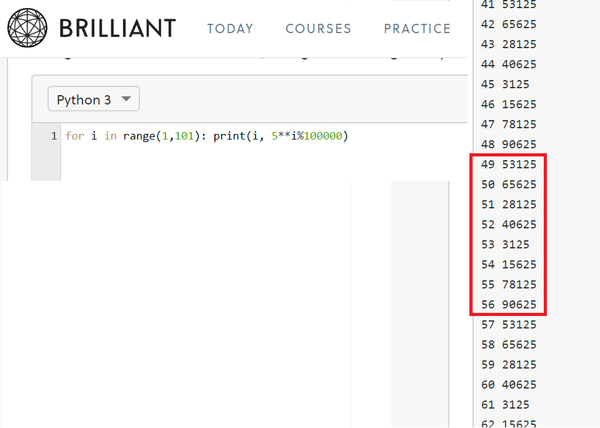
Any ideas for a truly calculator free method? (CRT looks good until you need to solve 3 2 n + 1 3 ≡ 0 ( m o d 3 1 2 5 ) .)
The "better pattern spotting" method I wrote up only needs multiplication of two digit numbers by 5 , but you do need to know that 2 6 = 1 5 6 2 5 , and realise what that means for the last three digits of 5 2 k . Of course, you can work that out, but it's hard to see what the motivation would be for that.
I used a calculator 😈😜. AND REKTED YOU ALL!
P. S. It was 7 8 1 2 5 . I used a calculator app and had to GODDAMN scroll for almost eternity[insert rage here] (aka. 3 seconds). P. P. S. All this writing is also taking almost eternity [insert more rage here](aka. 10 GODDAMN minutes)
What a solution! Never thought of that.
Can you provide a solution for the generalization of this problem, which means 5 n for every positive integers n ? Thanks in advance.
Method 1 : Chinese remainder theorem.
Method 2 : pattern spotting
We know that for n > 1 , the last two digits are always 2 5 .
Define a sequence a n by 5 n = 1 0 0 a n + 2 5 for n > 1 .
We have a 2 = 0 and 5 n + 1 = 1 0 0 a n + 1 + 2 5 = 5 0 0 a n + 1 2 5
so a n + 1 = 5 a n + 1 . We're only interested in the last three digits of this number, so we can ignore the others. The sequence goes 0 , 1 , 6 , 3 1 , 1 5 6 , 7 8 1 , 9 0 6 , 5 3 1 , 6 5 6 , 2 8 1 , 4 0 6 , 3 1 , 1 5 6 , 7 8 1 , 9 0 6 , ⋯
and we see it locks into a repeating cycle of 8 numbers. Using this pattern, we find the last three digits of a 5 5 are 7 8 1 so that the last 5 digits of 5 5 5 are 7 8 1 2 5 .
Method 3 : better pattern spotting
The last three digits of 2 5 n are 6 2 5 for n > 1 . Define 2 5 n = 1 0 0 0 b n + 6 2 5 ; we then get b 2 = 0 , b n + 1 = 2 5 b n + 1 5 , and we're only interested in the last two digits of b n .
Even better, b n is always a multiple of 5 , so 2 0 b n is always a multiple of 1 0 0 ; so we just need to keep track of the last two digits of b n ′ where b 2 ′ = 0 and b n + 1 ′ = 5 b n ′ + 1 5 .
The sequence we get is 0 , 1 5 , 9 0 , 6 5 , 4 0 , 1 5 , 9 0 ⋯ , which gets into a cycle of period 4 . So the last two digits of b 2 7 ′ are 1 5 ; the last five digits of 5 5 4 are 1 5 6 2 5 , and we get the same answer.
Method 4 : do you know your powers of 6 2 5 ?
There's an even stronger pattern in the last five digits of powers of 6 2 5 , though they're harder to work out without a calculator; this sequence is 6 2 5 , 9 0 6 2 5 , 4 0 6 2 5 , 9 0 6 2 5 , ⋯
From this, 5 5 2 ends in 4 0 6 2 5 , and we can multiply by 1 2 5 to get the answer.
Other methods:
Decimal expansions of 2 − n have the same digits as powers of 5 ( 0 . 5 , 0 . 2 5 , 0 . 1 2 5 , 0 . 6 2 5 , ⋯ ); is there a way to use this?