Find The Length
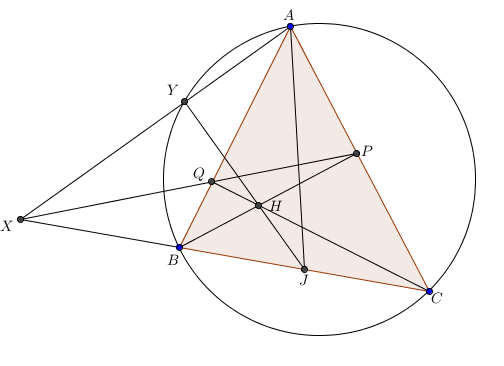 Let
△
A
B
C
be a triangle with
A
B
=
6
,
B
C
=
7
,
C
A
=
8
.
Let
P
,
Q
be the feet of perpendiculars from
B
,
C
on
C
A
,
A
B
respectively. Let
B
P
and
C
Q
meet at
H
,
and let
P
Q
and
B
C
meet at
X
.
Line
A
X
meets the circumcircle of
△
A
B
C
at
Y
,
where
Y
=
A
.
Lines
H
Y
and
B
C
intersect at
J
.
Given that
A
J
2
=
n
m
for some coprime positive integers
m
,
n
,
find
m
+
n
.
Let
△
A
B
C
be a triangle with
A
B
=
6
,
B
C
=
7
,
C
A
=
8
.
Let
P
,
Q
be the feet of perpendiculars from
B
,
C
on
C
A
,
A
B
respectively. Let
B
P
and
C
Q
meet at
H
,
and let
P
Q
and
B
C
meet at
X
.
Line
A
X
meets the circumcircle of
△
A
B
C
at
Y
,
where
Y
=
A
.
Lines
H
Y
and
B
C
intersect at
J
.
Given that
A
J
2
=
n
m
for some coprime positive integers
m
,
n
,
find
m
+
n
.
The answer is 155.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution; pretty direct. You could geometrically prove that J is the midpoint of B C (see my other comment) but I guess this is the natural approach.
Wow. Just... wow. Is this the intended solution? It's so long and there is so much calculation; I bet there is an easier way. We just need to prove that J is the midpoint of B C and we can easily find A J 2 by Stewart's theorem.
Log in to reply
Okay here goes the intended solution.
Let A ′ be the diametrically opposite point of A on the circumcircle of △ A B C . Note that A ′ B ⊥ A B ⟹ A ′ B ∥ C H and similarly A ′ C ∥ B H , so B A ′ C H is a parallelogram. Since the diagonals of a parallelogram bisect each other, H A ′ passes through the midpoint of B C .
Extend
A
′
H
to meet the circumcircle of
△
A
B
C
again at
Y
′
.
Since
H
Y
′
⊥
A
Y
′
,
H
Q
⊥
A
B
and
H
P
⊥
A
C
,
(
A
E
Q
H
P
)
is cyclic. Call this circle
ω
1
.
Also, points
B
,
C
,
P
,
Q
lie on the circle with diameter
B
C
.
Call this circle
ω
2
.
Finally, let
ω
3
be the circumcircle of
△
A
B
C
.
Let
rad
(
γ
1
,
γ
2
)
denote the radical axis of circles
γ
1
and
γ
2
.
Note that
rad
(
ω
1
,
ω
2
)
=
P
Q
rad
(
ω
1
,
ω
3
)
=
A
Y
′
rad
(
ω
2
,
ω
3
)
=
B
C
so by the radical axis theorem,
P
Q
,
A
Y
′
,
B
C
are concurrent at their radical center
X
.
Hence,
X
,
Y
′
,
A
are collinear, implying
Y
′
=
Y
.
This shows us that
Y
H
passes through the midpoint of
B
C
.
Log in to reply
A much simpler solution would be to let H ′ be the reflection of H about J . Note that A B H ′ C is a cyclic quadrilateral. We have
< B H ′ C = 1 8 0 − < B A C = < B H C
by the properties of the orthocenter , and so B H ′ C H is a parallelogram with diagonals H H ′ and B C ′ , thus implying that J is the midpoint of B C .
Note that the arguement that you provided can then be used to prove that H ′ and the A ′ in your solution coincide.
Yes, I noticed about it after submitting it, but I don't know why I always like to know the measure of every segment :D
By Stewart's theorem, like you say, we only had to find the length of the median A J :
A J = 2 2 ( A B 2 + A C 2 ) − B C 2 = 2 2 ( 3 6 + 6 4 ) − 4 9 = 2 1 5 1
Projective things like pole, polar, and harmonic division goes well too. ;)
Use Apollonius Theorem of triangles! It becomes a 3 liner!
Sorry for the late reply. Here's the background: Apollonius Theorem
A B 2 + A C 2 = 2 ( A J 2 + 0 . 5 B C 2 )
Therefore 6 2 + 8 2 = 2 ( A J 2 + ( 2 7 ) 2 ) .
Isolating A J 2 yields 4 1 5 1 .
151 + 4 = 155
Care to be more elaborate?
First let's calculate the area of △ A B C using Heron's formula: Δ = 4 ( 6 + 8 + 4 ) ( 6 + 8 − 4 ) ( 6 − 8 + 4 ) ( − 6 + 8 + 4 ) = 4 2 1 1 5 Find the length of the heights P B and Q C using the formula of the area of triangle knowing base and height:
Δ = 2 8 P B ⇒ P B = 1 6 2 1 1 5
Δ = 2 6 Q C ⇒ Q C = 4 7 1 5
Using Pythagorean theorem on △ B P C and △ B Q C , find P C and B Q respectively:
P B 2 + P C 2 = B C 2 ⇒ P C = 1 6 7 7
Q C 2 + B Q 2 = B C 2 ⇒ B Q = 4 7
Find A Q and A P :
A Q = A B − B Q = 4 1 7
A P = A C − P C = 1 6 5 1
Find cos ∠ B A C using cosines law:
cos ∠ B A C = 2 × A B × A C A B 2 + A C 2 − B C 2 = 3 2 1 7
Find P Q using again cosines law:
P Q 2 = A Q 2 + A P 2 − 2 A Q × A P × cos ∠ B A C ⇒ P Q = 3 2 1 1 9
Find cos ∠ B P Q :
cos ∠ B P Q = 2 × P Q × P B P Q 2 + P B 2 − B Q 2 = 4 1 5
Now, move to the right triangle △ P C B and find cos ∠ P C B :
cos ∠ P C B = B C P C = 1 6 1 1
Now, move to the triangle △ P X C :
We know that ∠ P X C + ∠ P C B + ∠ B P Q + 9 0 ° = 1 8 0 ° , so: cos ∠ P X C = cos ( 9 0 ° − ∠ P C B − ∠ B P Q ) = sin ( ∠ P C B + ∠ B P Q )
Use the Pythagorean identity and the double angle sum to find that sin ∠ P X C = 8 7
Use sines law to find B X :
sin ∠ P X C P C = sin ( 9 0 ° + ∠ B P Q ) B X + B C = cos ( ∠ B P Q ) B X + B C ⇒ B X = 8 2 1
Find cos ∠ A B C :
cos ∠ A B C = 2 × A B × B C A B 2 + B C 2 − A C 2 = 4 1
Now, move to the triangle △ A B X and find A X :
A X 2 = A B 2 + B X 2 − 2 × A B × B X × cos ( 1 8 0 ° ∠ A B C ) = A B 2 + B X 2 + 2 × A B × B X cos ∠ A B C ⇒ A X = 8 5 7
By Power of a Point, we know that X Y × A X = B X × ( B X + B C ) , so X Y = 1 5 2 5 3 9
Now, move to the triangle △ A X B and find cos ∠ A X B :
cos ∠ A X B = 2 × A X × B X A X 2 + B X 2 − A B 2 = 1 9 1 1
Now, move to the right triangle △ X Y J and find B J :
cos A X B = X J X Y = B X + B J X Y ⇒ B J = 2 7
Finally, move to the triangle △ A B J and find A J 2 :
A J 2 = A B 2 + B J 2 − 2 × A B × B J × cos ∠ A B C
A J 2 = 4 1 5 1
Hence, m = 1 5 1 , n = 4 and m + n = 1 5 5 .