Tangent Chord
The three colored circles above are tangent to each other, to chord A B , and to the large circle. The middle one has radius 5, and the other two on either side each have radius 4.
Find the length of chord A B .
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The flags were there in the original image. I've nothing to do with Bangladesh but the Indian flag is very dear to me.
Can you explain more on how you derived the two equations?
Log in to reply
Which two equations ?
You mean how to get A B 2 = 4 ( 2 5 2 − 1 5 2 ) ?
I don't know either, but i use 2 A B × 2 A B = ( 5 0 − 1 0 ) × 1 0 , which will also end up that A B = 4 0
What's with the India and Bangladesh Flag ? You come from there ?
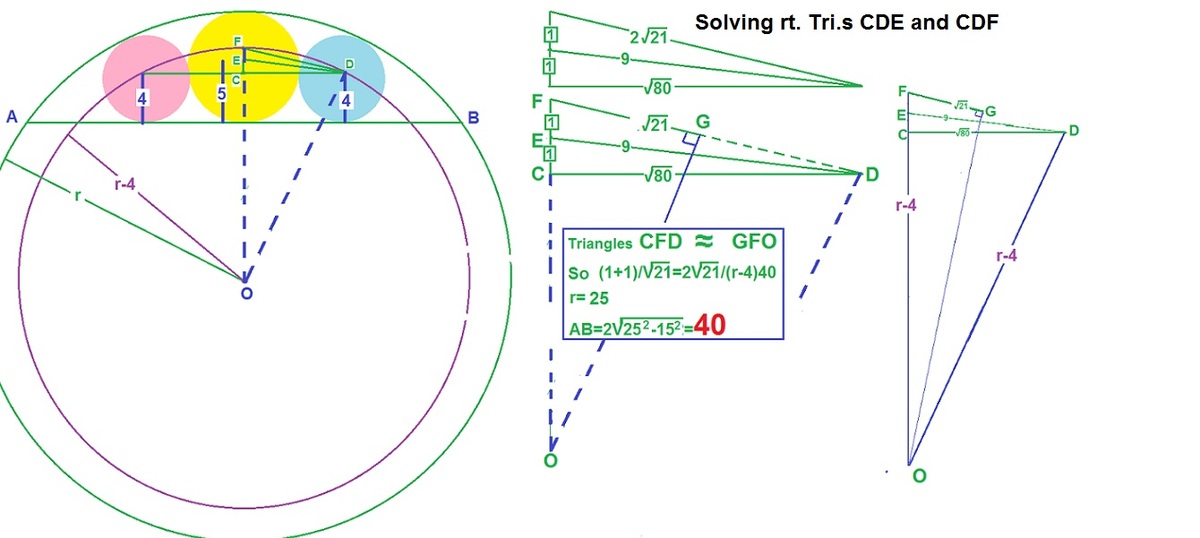
Let A B = l and R the radius of the large circle. We know that the length of the common tangent between the larger ( r = 5 ) and the smaller ( r = 4 ) circles is 2 5 × 4 or 2 2 0 . We now can write the following equations: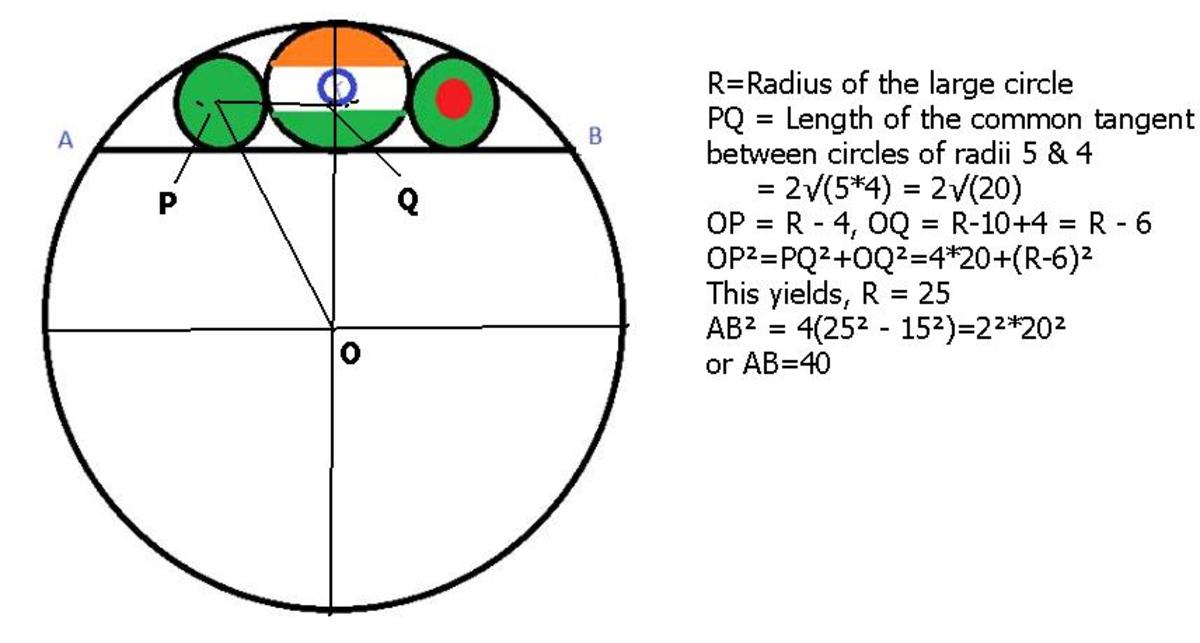
( R − 1 0 + 4 ) 2 + 4 × 2 0 ( l / 2 ) 2 = ( R − 4 ) 2 = R 2 − ( R − 1 0 ) 2
which yield R = 2 5 and l = 4 0 .