Find the length of the line
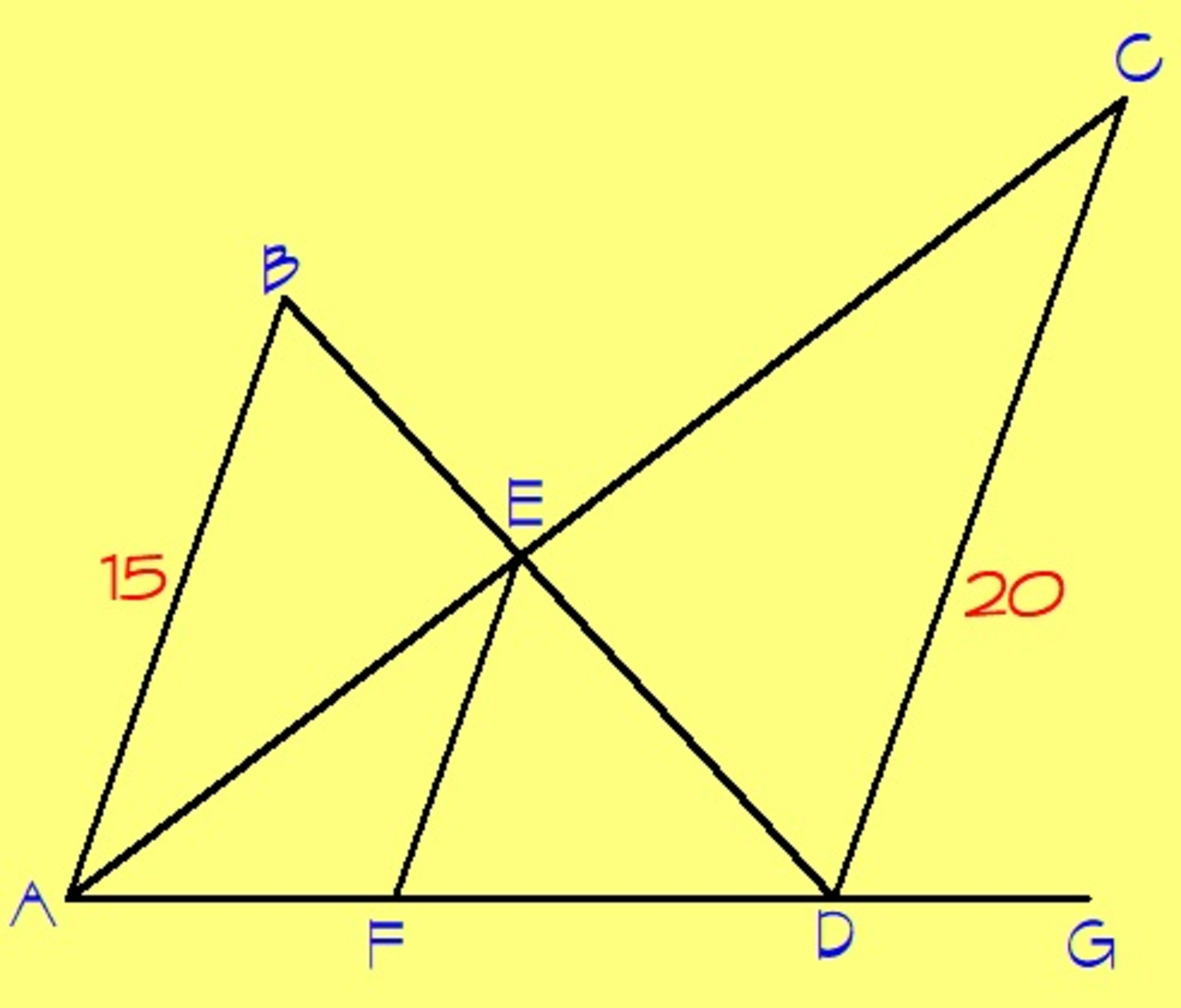 In the figure shown above,
. If
and
, find
. If your answer is of the form
where
and
are positive coprime integers, give
.
In the figure shown above,
. If
and
, find
. If your answer is of the form
where
and
are positive coprime integers, give
.
NOTE:
and are straight lines.
The answer is 14547.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since △ A C D ∼ △ A E F , we have: E F A F = D C A D ⟹ A F = 2 0 E F ( A D ) 1
Since △ B A D ∼ △ E F D , we have: E F E D = A B A D ⟹ F D = 1 5 E F ( A D ) ⟹ A D − A F = 1 5 E F ( A D ) 2
Substitute 1 in 2 , we have
A D − 2 0 E F ( A D ) = 1 5 E F ( A D )
Multiply both sides by the LCM of the denominators which is 6 0 .
[ A D − 2 0 E F ( A D ) ] 6 0 = [ 1 5 E F ( A D ) ] 6 0
6 0 A D − 3 ( E F ) ( A D ) = 4 ( E F ) ( A D )
6 0 A D = 7 ( E F ) ( A D )
E F = 7 6 0
The desired answer is ( 2 a ) 2 + 2 b 2 = ( 2 ⋅ 6 0 ) + 2 ( 7 2 ) = 1 4 5 4 7
Note:
I multiplied both sides of the equation by the LCM of the denominators which is 6 0 to remove the denominators (for easy calculation).
or you can do this
A D − 2 0 E F ( A D ) = 1 5 E F ( A D )
A D = 1 5 E F ( A D ) + 2 0 E F ( A D )
A D = 6 0 4 ( E F ) ( A D ) + 3 ( E F ) ( A D )
6 0 A D = 7 ( E F ) ( A D )
E F = 7 6 0
Which is the same, you must find the LCD so that the two fractions can be added.