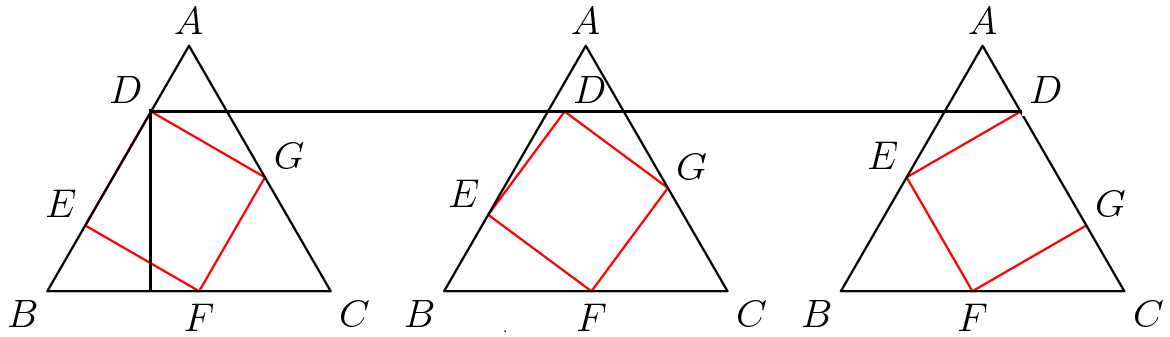
Find the length of the perpendicular to the base of this equilateral triangle.

Since the answer is apparently independent of the precise choices made, go for symmetry: make $BF = FC = \tfrac12$ , so that $D$ lies directly above $F$ .

We then know that in $\triangle BEF$ , $\angle B = 60^\circ$ , $\angle F = 45^\circ$ , from which $\angle E = 75^\circ$ .

With the Law of Sines, $\frac{EF}{\angle B} = \frac{BF}{\angle E} \therefore EF = \frac{\sin 60^\circ}{\sin 75^\circ}\cdot \tfrac12 = 0.44828\dots.$ This is the side of the square; the required perpendicular is $DF$ , the diagonal of the square; thus $DF = \sqrt 2 EF = \boxed{0.633974\dots}.$

It can be shown that the length of the perpendicular is a constant, regardless of how the square is positioned inside the triangle.

The required length is DC*sin(60).

DC = DG + GC,

DG is equal to sqrt(3)/2/(1 + sqrt(3)/2)

GC = (AC-DG)/2

We use coordinate geometry (with some complex numbers thrown in) to tackle the problem generally. Let $B = (0, 0), C = (1, 0), A = \left (\dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right ),$ and $F = (f, 0).$ The line $AB$ can be represented by the equation $y = \sqrt{3}x,$ and the line $AC$ can be represented by the equation $y = -\sqrt{3}(x - 1).$ Thus, if we let $g$ be the $x$ -coordinate of $G,$ then $G = (g, -\sqrt{3}(g - 1)).$

Interpret $F$ and $G$ as points in the complex plane i.e. $F = f, G = g - \sqrt{3}(g - 1)i.$ Point $E$ is a $90^{\circ}$ rotation counterclockwise of $G$ about $F,$ so

$E = i(G - F) + F = i((g - f) - \sqrt{3}(g - 1)i) + f = (f + \sqrt{3}(g - 1)) + (g - f)i.$

The corresponding point on the Cartesian plane is $E = (f + \sqrt{3}(g - 1), g - f.)$

Note that $E$ lies on $AB,$ which has the equation $y = \sqrt{3}x.$ Plugging in our coordinates for $E$ yields

$\begin{aligned} g - f &= \sqrt{3}(f + \sqrt{3}(g - 1)) \\ g - f &= \sqrt{3}f + 3(g - 1) \\ g &= \dfrac{3}{2} - \dfrac{1 + \sqrt{3}}{2}f. \end{aligned}$

Now, we must find the coordinates of $D$ ; specifically, we want only the $y$ -coordinate of $D,$ since the distance from $D$ to $BC$ is precisely that value. Let $DF$ and $EG$ intersect at $M.$ Since $DEFG$ is a square, $M$ is the midpoint of both $DF$ and $EG.$ The $y$ -coordinate of $M$ is

$M_y = \dfrac{(g - f) - \sqrt{3}(g - 1)}{2} = \dfrac{(1 - \sqrt{3})g - f + \sqrt{3}}{2},$

so the $y$ -coordinate of $D$ is

$D_y = 2 \left ( \dfrac{(1 - \sqrt{3})g - f + 3}{2} \right ) - 0 = (1 - \sqrt{3})g - f + \sqrt{3}.$

Substituting in the expression for $g$ we found earlier yields

$\begin{aligned} D_y &= (1 - \sqrt{3}) \left ( \dfrac{3}{2} - \dfrac{1 + \sqrt{3}}{2}f \right ) - f + \sqrt{3} \\ &= \dfrac{3(1 - \sqrt{3})}{2} - \dfrac{(1 - \sqrt{3})(1 + \sqrt{3})}{2}f - f + \sqrt{3} \\ &= \dfrac{3 - 3 \sqrt{3}}{2} + f - f + \sqrt{3} \\ &= \dfrac{3 - 3 \sqrt{3}}{2} + \sqrt{3} \\ &= \dfrac{3 - \sqrt{3}}{2} \\ &\approx \boxed{0.634}, \end{aligned}$

which is our final answer.

Drop a perpendicular from E to BC and let that line intersect BC at point M. Drop a perpendicular from G to BC and let that line intersect BC at point N. Let the length of EM be a and the length of GN be b. The question is basically asking us to find what a+b is (this can be seen by circumscribing a larger square around square DEFG with MN as one of its sides). BM=a/sqrt(3) and CN=b/sqrt(3) MF=b and NF=a. BM + MF + NF + CN = a/sqrt(3) + b + a + b/sqrt(3) =1.
a(1+1/sqrt(3)) + b(1+1/sqrt(3)) =1 (a+b)(1+1/sqrt(3))=1 a+b=1/(1+1/sqrt(3))

Let $x$ be the measurement of $\angle CFG$ , $s$ be the length of the side of the square, and $H$ be the point of intersection of the perpendicular from point $D$ to segment $BC$ .

Since $\triangle ABC$ is an equilateral triangle, $\angle B = 60°$ and $\angle C = 60°$ , and since $DEFG$ is a square, $\angle EFG = 90°$ .

Since the angle sum of $\triangle FGC$ is $180°$ , $\angle FGC = 180° - 60° - x = 120° - x$ . Then by the law of sines on $\triangle FGC$ , $\frac{\sin(120° - x)}{FC} = \frac{\sin 60°}{s}$ , which rearranges to $FC = \frac{s}{\sin 60°}\sin(120° - x)$ .

Since a straight line is $180°$ , $\angle BFE = 180° - 90° - x = 90° - x$ . Since the angle sum of $\triangle BEF$ is $180°$ , $\angle BEF = 180° - 60° - (90° - x) = 30° + x$ . Then by the law of sines on $\triangle BEF$ , $\frac{\sin(30° + x)}{BF} = \frac{\sin 60°}{s}$ , which rearranges to $BF = \frac{s}{\sin 60°}\sin(30° + x)$ .

Since each side length of the equilateral triangle $\triangle ABC$ is $1$ , $BF + FC = 1$ , and substituting the above equations for $BF$ and $FC$ gives $\frac{s}{\sin 60°}\sin(30° + x) + \frac{s}{\sin 60°}\sin(120° - x) = 1$ , which simplifies to $s(\sin x + \cos x) = \frac{3 - \sqrt{3}}{2}$ .

Since $DF$ is a diagonal of the square $DEFG$ with side lengths of $s$ , $DF = \sqrt{2}s$ , and angle $\angle DFG = 45°$ . Since a straight line is $180°$ , $\angle BFD = 180° - 45° - x = 135° - x$ . Since $\triangle DHF$ is a right triangle, $\sin(135° - x) = \frac{DH}{\sqrt{2}s}$ , which simplifies to $DH = s(\sin x + \cos x)$ .

Therefore, since $DH = s(\sin x + \cos x)$ and $s(\sin x + \cos x) = \frac{3 - \sqrt{3}}{2}$ , $DH = \frac{3 - \sqrt{3}}{2} \approx \boxed{0.633974596}$ , and is constant regardless of the placement of square $DEFG$ .

As the height of $D$ is apparently independent of the orientation of the square, we can orient it as such to align $D$ directly above $F$ , and use Pythagorean Theorem to easily find a solution:

In this symmetrical orientation, we know $AEG$ is an equilateral triangle since $EG$ is parallel to $BC$ , and it has a side length of $DF$ . The height of an equilateral triangle is equal to $\frac{\sqrt3}{2}$ multiplied by its side length, so we know that the height of triangle $ABC$ is $\frac{\sqrt3}{2}$ , the height of the triangle $AEG$ is $\frac{DF\sqrt3}{2}$ , and the height of trapezoid $EBCG$ is $\frac{DF}{2}$ . This means $\frac{DF\sqrt3}{2}+\frac{DF}{2}=\frac{\sqrt3}{2}$ , which can be rearranged to $DF=\frac{\sqrt3}{\sqrt3+1}$ , which gives us $DF\approx\boxed{0.634}$ .

I used a ruler... segment BC equeled 10 cm and the perpendicular segment measured to be 6.5 cm (I wrote .65 for the answer and got it on the first try.)