Find the length!
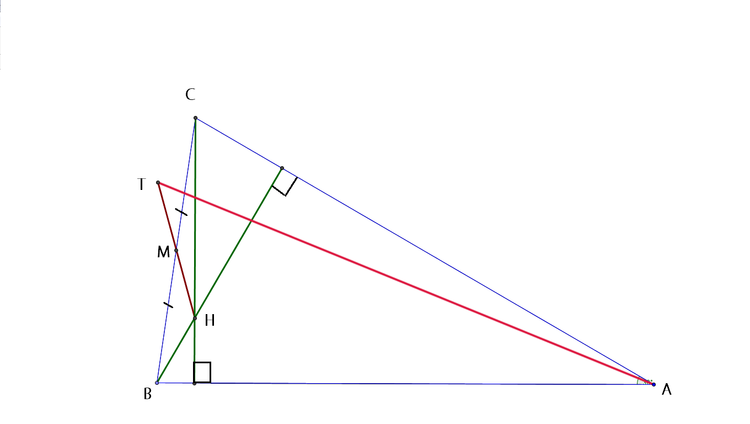 △
A
B
C
is an acute angled triangle with
∠
A
=
3
0
∘
and
B
C
=
5
cm.
H
is the orthocentre, and
M
is the midpoint of
B
C
.
T
is a point on the line
H
M
such that
H
M
=
M
T
. Find the length of
A
T
in centimetres.
△
A
B
C
is an acute angled triangle with
∠
A
=
3
0
∘
and
B
C
=
5
cm.
H
is the orthocentre, and
M
is the midpoint of
B
C
.
T
is a point on the line
H
M
such that
H
M
=
M
T
. Find the length of
A
T
in centimetres.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Care to correct your typo? You asked for AC instead of AT . -_-
What type of quadrilateral is T A H C ?The order in which you name the vertices makes it look more like a triangle with a stick protruding from it.
Log in to reply
Is there anything wrong with the diagram,or am I reading things the wrong way?
Really very sorry. In the first line, we join T , B instead of T , A and T B H C , not T A H C
U should have waited.... i was then locked inside a little room answering to natures call! -_-
This question uses a fact that orthocentre reflected about a midpoint always lies on a circumcircle, on a diameter of circumcircle with opposite vertex as the other end of the diameter.
Let R denote radius of circumcircle, O its circumcentre. In this case it means that A T = 2 R . By inscribed angle theorem ∠ B O C = 2 × ∠ B A C = 6 0 ⇒ △ B O C is equilateral ⇒ R = B C = 5 ⇒ A T = 1 0 .
it's not a proof, you solved only this case and fortunatly you get the correct result.

We join B , T and T , C . Thus in quadrilateral T B H C we have the diagonals bisecting each other whcih implies T A H C is a parallelogram. Thus, A H = T C and T C ∥ A C which means ∠ T C A = 9 0 ∘ . Now, let O be the circumcentre of △ A B C and as △ A B C is acute, O lies inside the triangle. WE drop O X ⊥ A C .
Now, O X = 2 1 × A H = 2 1 × T C . And along with that T C ∥ O X and X is the midpoint of A C . This implies O is the midpoint of A T and thus A T is the diameter of the circumcircle of △ A B C . Finally we use the extended Law of Sines in △ A B C which yields
sin ∠ A B C = 2 R , where R is the circumradius of △ A B C
⟹ sin 3 0 ∘ 5 = A T
⟹ A T = 1 0