Find the limit!

tried to do in a little rigorous procedure

First, let's get some key insights on the function $f(x)$ and $g(x)$ .

$\int_{0}^{3} f(t) dt = 6$ $\dfrac{\text{d}g}{\text{d}x} = f(x)$

Using the definition of an integral, we glean that:

$g(3)-g(0)=6$ $g(0)=0$ $g(3)=6$

Now, let's think practically. Sure, there are some sine and cosine waves that work with these formulas, so if you want to use these, be my guest:

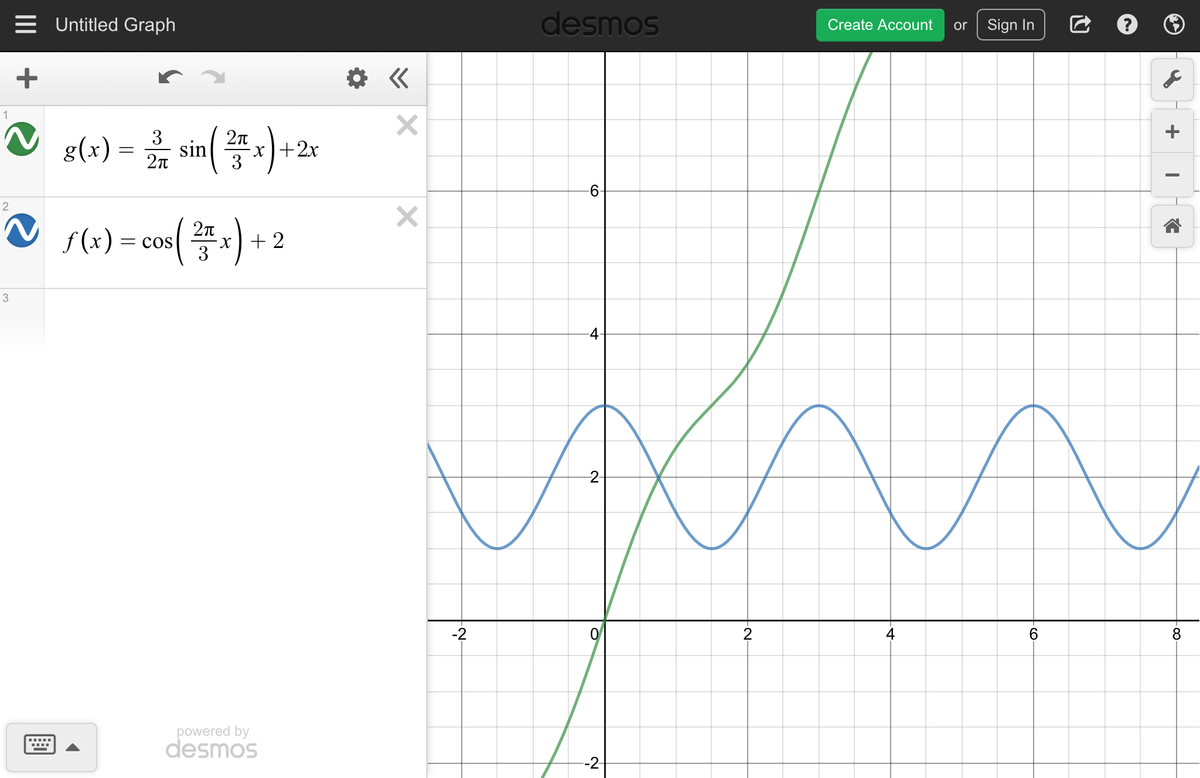Ugly Sine Waves

I'm going to use the practical way. The line that passes through the points $(0, 0)$ and $(3, 6)$ is $g(x)=2x$ . $\dfrac{\text{d}g}{\text{d}x} = 2 = f(x)$ . Surprisingly, this function satisfies the rest of the requirements! The integral will be just the area of a rectangle with side lengths $2$ and $3$ , which will be $6 \text{ units}^{2}$ . And because it's a constant function, $f(x)=f(x+3)$ , so this function technically speaking has a period of $3$ .

The rest is computation:

$\lim_{x\rightarrow 0} xg(\dfrac{1}{x})=$ $\lim_{x\rightarrow 0} x\dfrac{2}{x}=$ $\lim_{x\rightarrow 0} 2=$ $\boxed{2}$

Our answer is $\boxed{2}$ .