Find The Limiting Ratio
Beginning with a square of area 1, construct a sequence of rectangles by alternately adjoining a rectangle of area one alongside or on top of the previous rectangle. First five rectangles are shown:
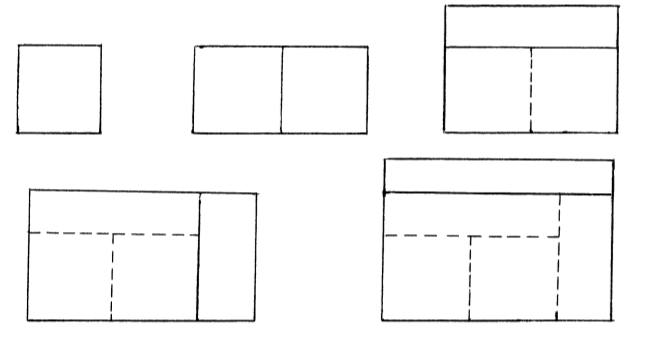
The limiting ratio of length to height has a closed form. Find this closed form.
Give your answer to 3 decimal places.
Source : Gerald Myerson (Elementary Problems, American Mathematical Monthly).
The answer is 1.570796.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Limits of Sequences - Medium
Let x n be the total length of the rectangle when n − 1 rectangles has contributed to the length.
Let y n be the total height of the rectangle when n rectangles has contributed to the height.
Through considering the area of the rectangle,
x n y n = 2 n
x n − 1 y n = 2 n − 1
With initial conditions: x 1 = 2 , y 1 = 1
Solving these recurrence relations gives
x n = 2 2 n ( 2 n ) ! ( n ! ) 2
y n = ( n ! ) 2 2 1 − 2 n n ⋅ ( 2 n ) !
y n x n = n ⋅ ( ( 2 n ) ! ) 2 2 4 n − 1 ( n ! ) 4
Using these and Stirling's approximation gives
n → ∞ lim y n x n = 2 π