Find the max of complex number

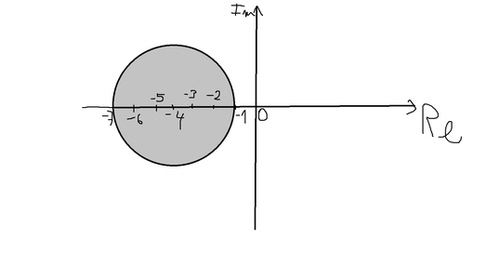
Similar solution with @Dan Czinege with more details

Let the complex number $z=x+iy$ , where $x$ and $y$ are real numbers and $i=\sqrt{-1}$ denotes the imaginary unit . Then $|z+4| \le 3$ , implies that $(x+4)^2+y^2 \le 3^2$ , which is a circle (red) with center at $(-4,0)$ and radius of $3$ in the complex plane. All $z$ sastifying $|z+4| \le 3$ is within the red circle. Therefore all the $z+1$ are within a circle of the same radius shifted by $+1$ or with center at $(-3,0)$ (the blue circle). Then $\max |z+1| = \boxed 6$ , when $z+1 = -6$ the point farthest away from the origin $(0,0)$ .

The grey circle represents all numbers with the property $|z+4|<=3$ and if we must find maximum of $|z+1|$ it means we must find maximum distance of some number of grey circle to number -1 and thus it is 6.