Find the max value of y

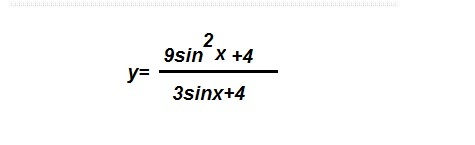
No need for derivatives. Just try to maximize numerator and minimize denominator.

$\sin^{2}x$ is always positive and its maximum is $1$ at $x = \dfrac{\pi}{2} + k\pi$ where $k = 0, 1, 2, ...$ , while $\sin x$ has minimum of $-1$ at $x = \dfrac{3\pi}{2} + 2k\pi$ where $k = 0, 1, 2, ...$ . At those points $y = \frac{9\sin^{2} x + 4}{3\sin x + 4} = \frac{9+4}{-3+4} = 13.$