Find the Maximum Value
Algebra
Level
2
Find the maximum value of 5X + 4Y such that
2X + 3Y <= 7
and
2X - Y <= 2
and
X,Y are >= 0.
13.125
0
9.333
5
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
These two equations
2X + 3Y <= 7
2X - Y <= 2 can be graphically represented as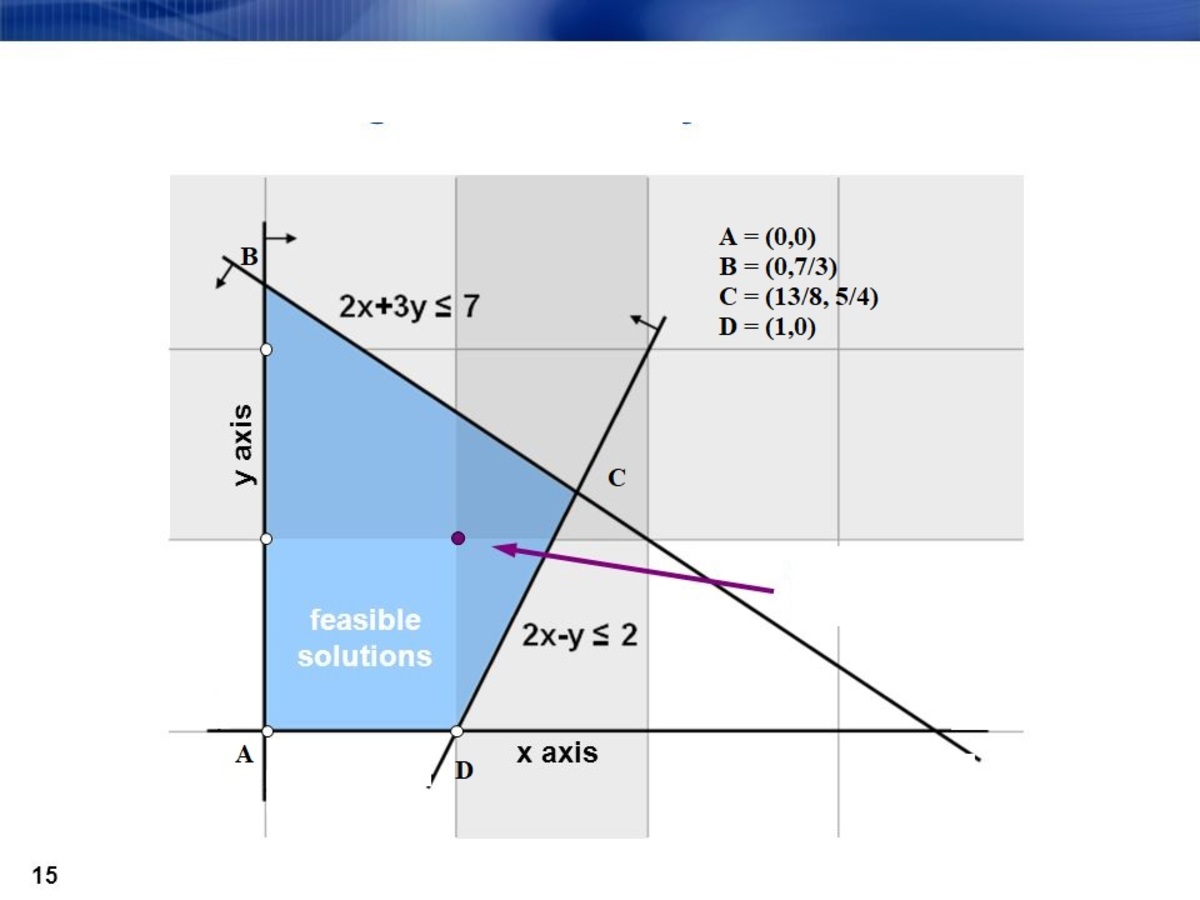
The maximum or minimum value of 5X + 4Y will fall on the vertices of the feasible region A, B , C or D as ABCD is a convex polytope.
So calculating the value of 5X + 4Y at A, B, C and D respectively yields a maximum value of 13.125 at Point C. The above is an example of a Linear Programming Problem ,simple formulations of which can be solved graphically. Linear Programming .
It can also be verified randomly that any point inside the polytope ABCD such as (1,1) will yield a smaller value of the objective function than the maximum or extreme value which will fall on the vertex. In fact the minimum value of 5X + 4Y (objective function) will fall on another vertex A. Value 0.