Find the maximum value of ∠OMA
Let O be the origin of the Cartesian coordinate, given a circle C : x 2 + y 2 = 8 , and a point A ( 2 , 0 ) . Let M be an arbitrary point on circle C . What is the maximum value of ∠ O M A (in degrees)?
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Alice Smith , we use backslash "\" a lot in LaTex. For examples: \triangle △ , \angle ∠ , \in ∈ , \frac \pi 2 2 π , \dfrac 3{23} 2 3 3 , \sin \alpha sin α , \cos \beta cos β , \tan \gamma tan γ , \ln x ln x , \int 0^\frac \pi 2, \sum {k=0}^\infty (there is an underscore after \int and \sum not shown on screen here), \frac 12 ∫ 0 2 π , ∑ k = 0 ∞ , 2 1 and put them after \displaystyle \int 0^\frac \pi 2, \sum {k=0}^\infty, \frac 12 ∫ 0 2 π , k = 0 ∑ ∞ , 2 1 . We need only one \displaystyle in front. If you are using \ [ ⋯ \ ] instead of \ ( ⋯ \ ) , you don't need \displaystyle.
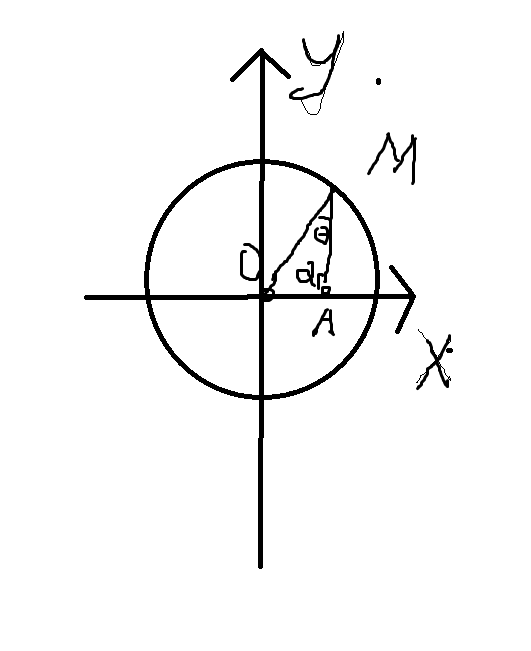 In the triangle OMA , we will get
s
i
n
Θ
2
=
s
i
n
α
2
2
,because of the sine theorem.
In the triangle OMA , we will get
s
i
n
Θ
2
=
s
i
n
α
2
2
,because of the sine theorem.
Observing this equation, we will find that sinα gets maximum value when Θ get maximum value.
So when MA is perpendicular to x-axis,we get the maximum value of ∠OMA .
We can easily figure out that sinΘ =
2
2
.
hence, the maximum value of ∠OMA=45°
Consider the △ O M A . We note that O M = 2 2 , the radius of circle C , and O A = 2 , the x -coordinate of A . Let ∠ O M A = θ and ∠ M A O = α . By sine rule , we have:
O A sin ∠ O M A 2 sin θ ⟹ sin θ = O M sin ∠ M A O = 2 2 sin α = 2 sin α
For 0 ∘ ≤ θ ≤ 9 0 ∘ , the larger θ , the larger sin θ and θ is maximum when sin θ is maximum or when sin α = 1 . Then max ( sin θ ) = 2 1 ⟹ max ( θ ) = 4 5 ∘ .