∠ C = ?
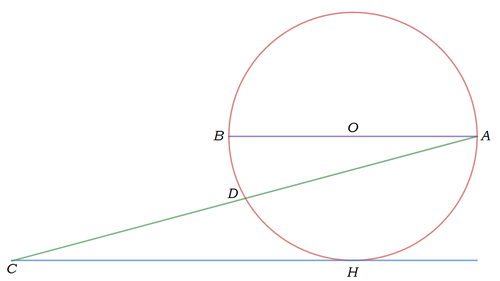
Line A B , a diameter of circle with center O , is parallel to C H , which is tangent to the circle. A C intersects the circle at D such that A D = C D . Find the measure of ∠ A C H in degrees.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
By Thales theorem angle ADB is 90°. And because D is midpoint of line segment AC we can say that triangle ACB is isosceles. Now because angle ACH is congruent to angle CAB and triangle ACB is isosceles we can say that angles CAB and BCA are congruent too, thus line CA is angle bisector of angle BCH.
Let E be the foot of perpendicular from B to line CH and let
r
be the radius of the circle. We now know that
∣
B
E
∣
=
r
and
∣
C
B
∣
=
∣
B
A
∣
=
2
r
, from this we can easily calculate that the angle BCE is 30° and thus
∣
A
C
H
∣
=
2
1
∣
B
C
H
∣
=
1
5
°
.
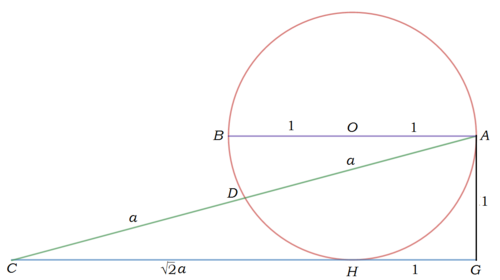
Let the radius of circle O be 1 and A D = C D = a . Then the height of △ A C G , A G = 1 . By tangent-secant theorem , we have C H 2 = C A ⋅ C D = 2 a 2 ⟹ C H = 2 a . By Pythagorean theorem ,
A G 2 + C G 2 1 2 + ( 1 + 2 a ) 2 1 + 1 + 2 2 a + 2 a 2 a 2 − 2 a − 1 ⟹ a sin ∠ A C H ⟹ ∠ A C H = A C 2 = ( 2 a ) 2 = 4 a 2 = 0 = 2 2 + 6 = A C A G = 2 + 6 1 = 1 5 ∘ Since a > 0
Let the radius of the circle be r and magnitude of ∠ A C H be α . Then, since ∠ B D A , being a semicircular angle, is 9 0 ° , ∣ A D ∣ = 2 r cos α ⟹ ∣ A C ∣ = 4 r cos α . Applying sine rule to the △ A C H we get sin 1 3 5 ° 4 r cos α = sin α r 2 ⟹ sin 2 α = 2 1 ⟹ 2 α = 3 0 ° ⟹ α = 1 5 ° .