Find the missing area
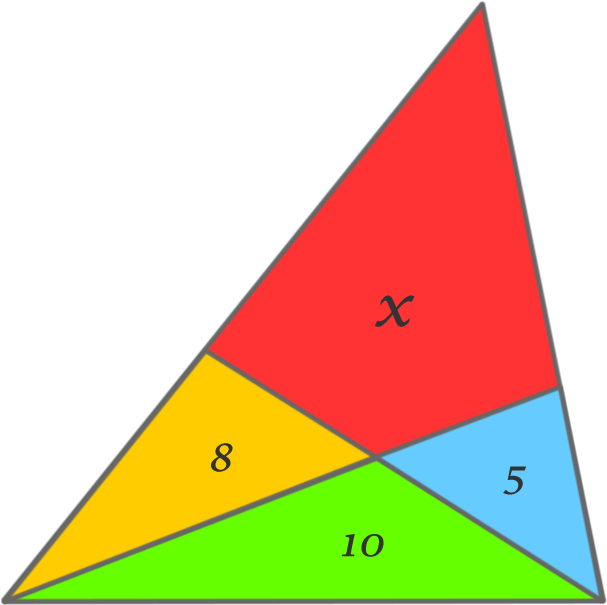
The areas of each portion of the triangle are given.
Find the value of x .
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Neat and sweet!
Simple and elegant! How did you form the equations though?
Log in to reply
Since the triangle having areas ( 8 + a ) and b share an apex, and their bases are along the same line, then the ratio of their areas is the same as the ratio of their bases lengths. The same bases are shared by the 10 and the 5 triangles which also have a common apex. It follows that the ratio of 5 1 0 = ratio of bases = b 8 + a . The same logic can be applied to the triangles having areas ( 5 + b ) and a on one side of the line and 1 0 and 8 on the other side of the line.
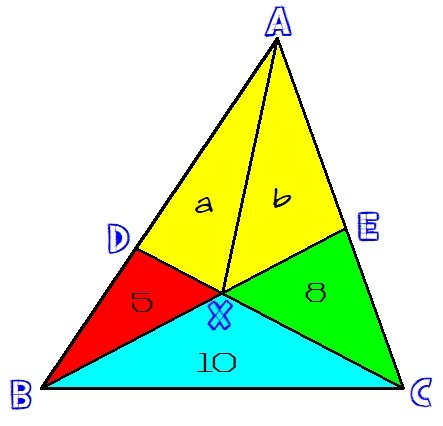 Consider the diagram. Recall that the areas of triangles with equal altitudes are proportional to the bases of the triangles. We have,
D
B
A
D
=
A
C
D
B
A
C
D
A
=
A
X
D
B
A
X
D
A
Consider the diagram. Recall that the areas of triangles with equal altitudes are proportional to the bases of the triangles. We have,
D
B
A
D
=
A
C
D
B
A
C
D
A
=
A
X
D
B
A
X
D
A
5 + 1 0 a + b + 8 = 5 a ⟹ 5 ( a + b + 8 ) = 1 5 a ⟹ a + b + 8 = 3 a ⟹ b + 8 = 2 a ( 1 )
E C A E = A B E C A A B E = A E X C A A X E
8 + 1 0 a + b + 5 = 8 b ⟹ 8 ( a + b + 5 ) = 1 8 b ⟹ 4 a + 4 b + 2 0 = 9 b ⟹ 4 a + 2 0 = 5 b ( 2 )
Substitute ( 1 ) in ( 2 ) , we have
2 ( b + 8 ) + 2 0 = 5 b ⟹ 2 b + 1 6 + 2 0 = 5 b ⟹ 3 6 = 3 b ⟹ 1 2 = b
It follows that,
2 a = b + 8 = 1 2 + 8 = 2 0 ⟹ a = 1 0
Finally, the desired area is a + b = 1 0 + 1 2 = 2 2
NOTE: My diagram is no true to scale.
The first stage of this solution could probably be avoided but I am yet to find the shortcut.
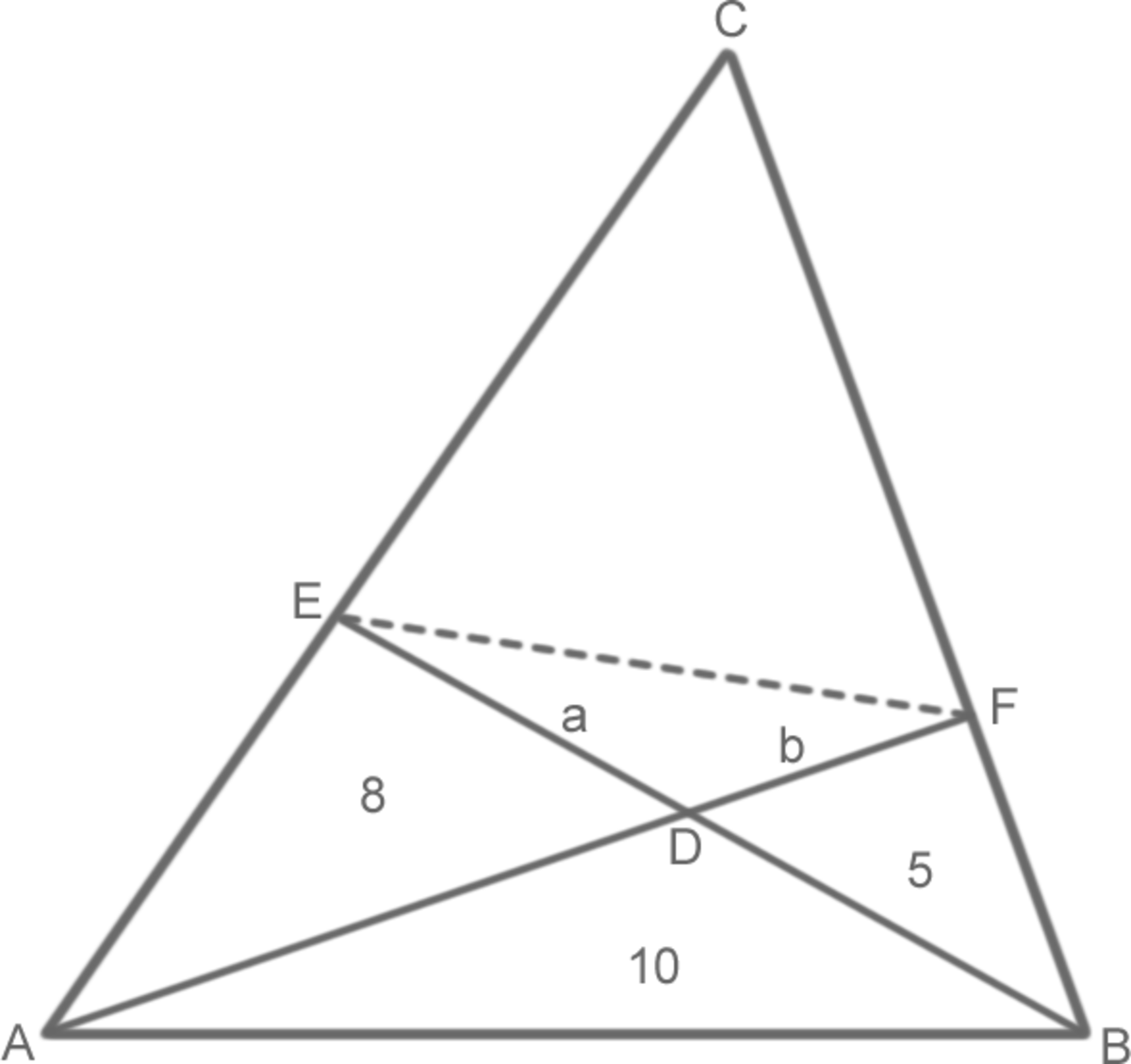
Areas: △ A D E = 8 , △ B D F = 5 and △ A B D = 1 0 . Let D E = a and D F = b .
Since △ A B D and △ A D E share the same height (perpendicular to E B ), then D B must be equal to 8 1 0 a = 4 5 a .
Using similar logic on △ A B F , you can show that A D = 2 b .
Since ∠ A D B = ∠ E D F , we can use the ratios between the sides of △ A B D and △ D E F to work out the area of △ D E F . D E × D F = a b , whilst A D × B D = 4 5 a × 2 b = 2 5 a b ⟹ △ D E F × 2 5 = △ A B D = 1 0 ⟹ △ D E F = 4 .
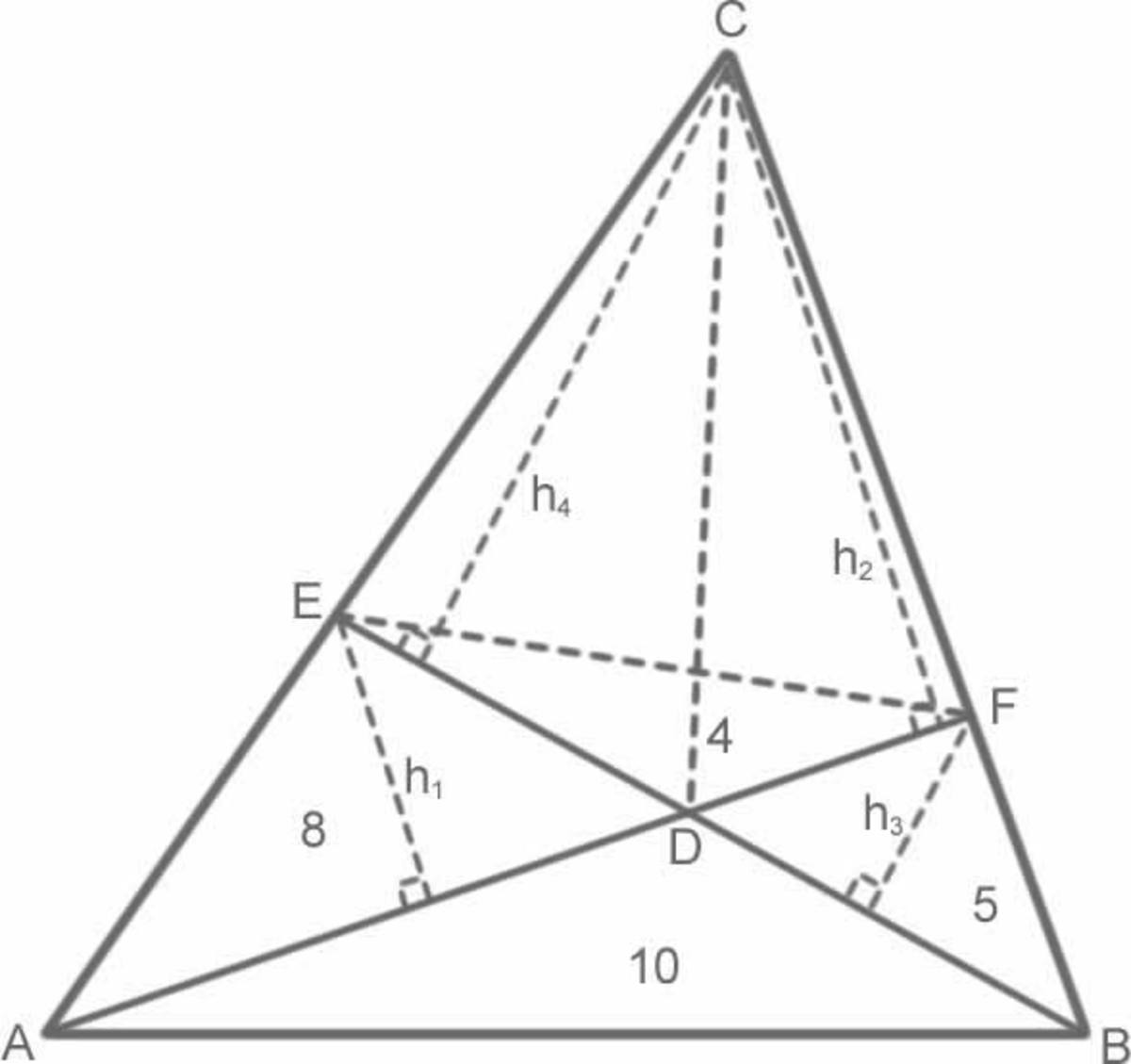
Let the heights of triangles △ A D E , △ A C F , △ B D F , and △ B C E be h 1 , h 2 , h 3 and h 4 respectively. Then define the ratios h 2 h 1 = x and h 4 h 3 = y .
Because they share the same base ( A D ), the area of △ A C D = x △ A D E = 8 x , and so by subtraction the area of △ C D E = 8 x − 8 . Applying this to △ B D F , △ B C D and △ C D F , you can show also that △ C D F = 5 y − 5 .
△ C D E and △ D E F share base D E , so y △ D E F = △ C D E = 4 y . △ D E F and △ C D F share base D F , so x △ D E F = △ C D F = 4 x .
Equating the expressions for △ C D E gives 4 y = 8 x − 8 ⟹ 5 y = 1 0 x − 1 0 and then for △ C D F gives 5 y − 5 = 4 x ⟹ 5 y = 4 x + 5 .
Thus, 1 0 x − 1 0 = 4 x + 5 ⟹ x = 2 5 .
The area of quadrilateral C E D F = △ C D E + △ C D F = 8 x − 8 + 4 x = 1 2 x − 8 = 3 0 − 8 = 2 2 .
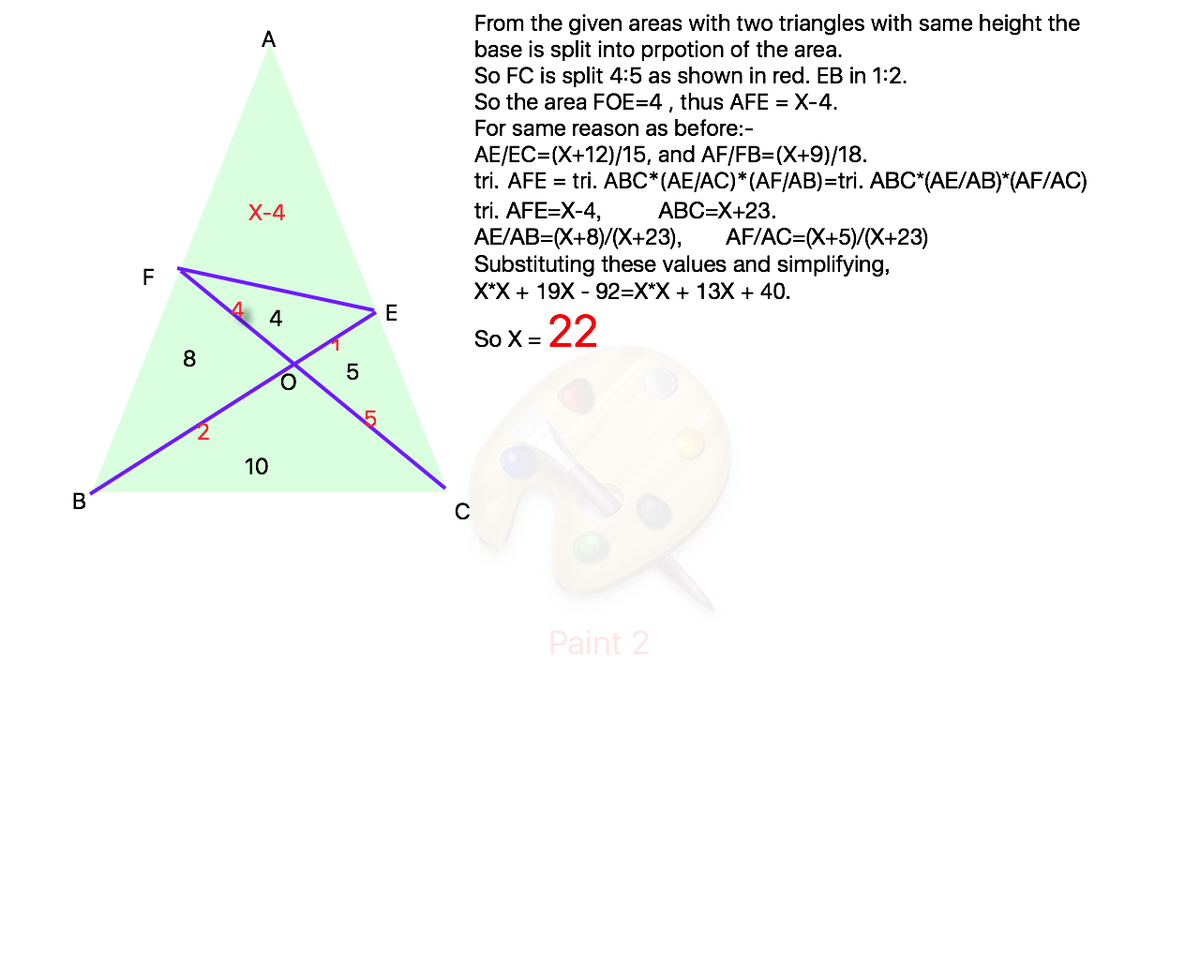
Split the area labelled X into two areas as shown in the above figure, with areas a and b . It follows that
b ( 8 + a ) = 5 1 0 = 2
and
a ( 5 + b ) = 8 1 0 = 4 5
From the above two equations, we get
a − 2 b = − 8
and
5 a − 4 b = 2 0
Solving this system of equations, results in a = 1 2 and b = 1 0 , Hence x = a + b = 1 2 + 1 0 = 2 2 .