Find the next augmenting path for Edmonds-Karp
In the Edmonds-Karp algorithm , the set of augmenting paths to choose from is well defined. Which of the following options will be the next augmenting path chosen by Edmonds-Karp?
The following graph shows a set of vertices and edges. Each edge shows two numbers: its current flow divided by its capacity. In this implementation, vertices are processed in alphabetical order for search.
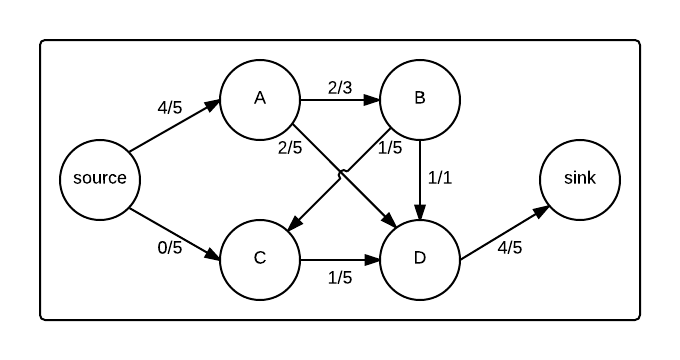Graph in the middle of Edmonds-Karp
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Doing breadth first search, first iterates all the neighbours of source. Both edges source-A and source-C have available flow. Hence both vertices A and C are added to queue (going alphabetically) : [(s)A,(s)C]. Next, A is picked from the queue, and we find edges A-B and A-D available; we add these two to the queue : [(s)C,(sA)B,(sA)D]. Next C is picked and its available edges are backward edge to vertex B and forward edge to D. We add these to queue : [(sA)B,(sA)D,(sC)B,(sC)D]. Next B is picked with edges going to C and D, changing queue to : [(sA)D,(sC)B,(sC)D,(sAB)C,(sAB)D]. Next we pick D, with forward edge to sink, and backward edges to B and C. Since sink is found we stop with our desired shortest path : s-A-D-s. (Parenthesis in queue are used to save the path).