Find the orange area!
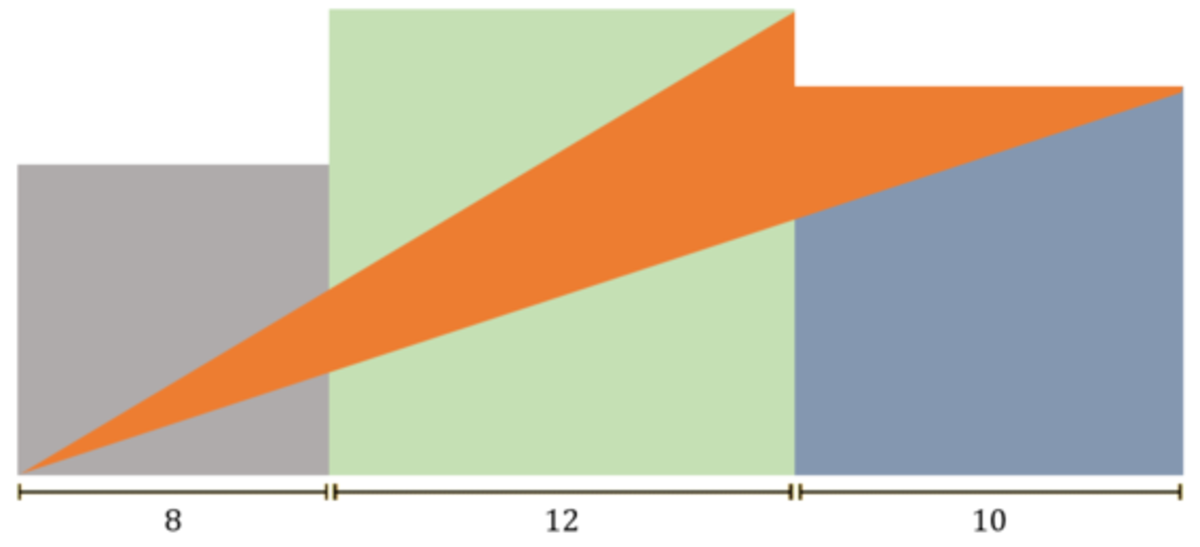
Three squares of side lengths 8 , 1 2 , and 1 0 are placed side-by-side as shown. Find the area of the orange region.
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Excellent, Sir!
Though i calculated each area of trapezium using analytic geometry of slopes and all, your's is much more clean, Nice!
Log in to reply
I did not know how to solve it even though I posted it! :)
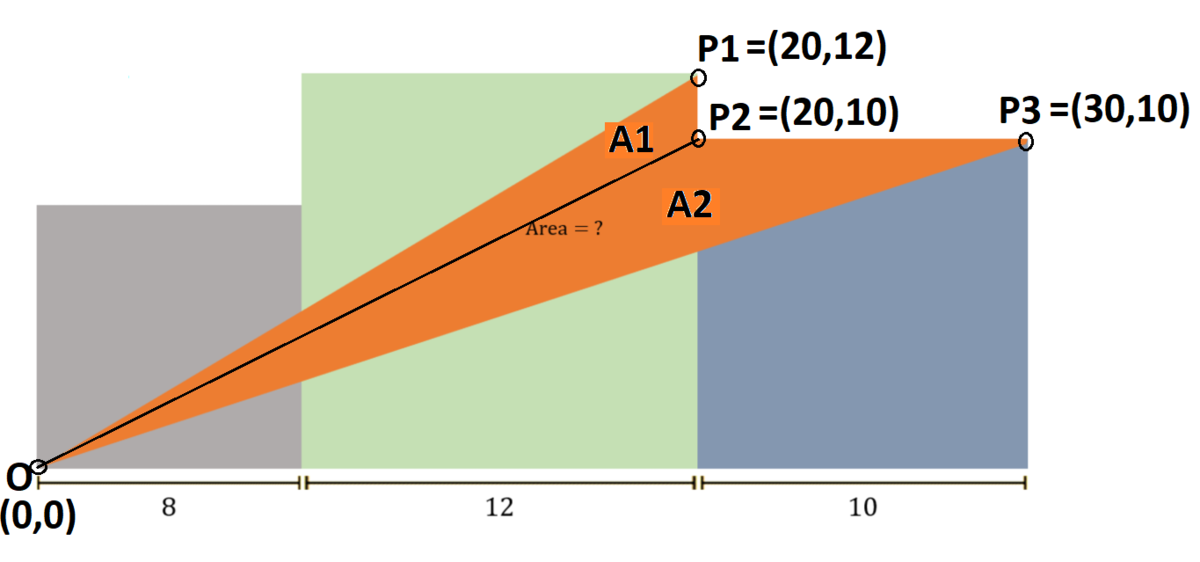
Define the points as shown and use the cross product formula for the area of a triangle. Calculate the areas of the two sub-triangles as shown, and combine them. The area comes out to 7 0 .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
Nice solution but I was thinking that if it is possible to find a solution only by elementary geometry?
Log in to reply
Yes, you can also do:
A = 2 1 ( 1 0 ) ( 1 0 ) + 2 1 ( 2 ) ( 2 0 ) = 7 0
Log in to reply
Thanks a lot! This problem was confusing me too much.
Area of figure = a r ( A B C ) + a r ( C B D ) - a r ( g r e e n r e c t a n g l e )
Area of figure = 2 1 ∗ 1 0 ∗ 1 2 + 2 1 ∗ 2 ∗ 3 0 − 1 0 ∗ 2
Area of figure = 7 0
Log in to reply
Nice solution!
Log in to reply
@Vinayak Srivastava ,the previous solution was wrong.
Thanks.How you have done it ?.
Log in to reply
I did not do it :) I did not know I how to do it, actually.
Redraw the figure above without affecting the orange region. We find the orange region is given by:
A = 3 0 × 1 2 − 2 3 0 × 1 0 − 2 2 0 × 1 2 − 1 0 × 2 = 3 6 0 − 1 5 0 − 1 2 0 − 2 0 = 7 0