Find the Radius

Geometry Level 5

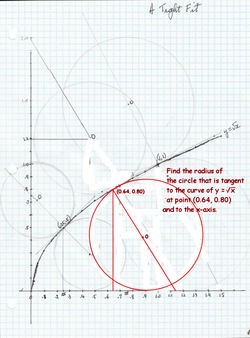Let r r be the radius of the circle that is tangential to the curve y = x y = \sqrt{ x} at the point ( 0.64 , 0.80 ) (0.64, 0.80 ) , and the x-axis.

What is 10000 × r 10000 \times r ? Please check below for a larger image.


The answer is 4329.

Guiseppi Butel by Guiseppi Butel , 90, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Pranjal Jain
Oct 4, 2014

Let point of tangency be P. f ( x ) = x f(x)=\sqrt{x}

f ′ ( x ) = 1 2 x = 5 8 f'(x)=\frac{1}{2\sqrt{x}}=\frac{5}{8}

t a n θ tan \theta = 5 8 \frac{5}{8} ⟹ c o s θ \implies cos \theta = 8 89 \frac{8}{\sqrt{89}} where θ \theta is angle between tangent at P and horizontal or angle between PO and vertical. Let foot of perpendicular from P on vertical radius be M.

R + O M = R + O P cos ⁡ θ = R ( 1 + cos ⁡ θ ) = y = 0.8 R+OM=R+OP \cos \theta=R(1+\cos \theta)=y=0.8

R = 0.8 1 + 8 89 ≈ 0.4329 R=\frac{0.8}{1+\frac{8}{\sqrt{89}}}≈0.4329

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Pranjal Jain, I'm not sure where M is. A diagram would be helpful. Thanks.

Guiseppi Butel - 6 years, 8 months ago

P = ( . 64 , . 8 ) . L e t t a n g e n t f r o m P m e e t x − a x i s a t S . L e t f ( x ) = x . S l o p e m o f S P , s a y t a n θ = f ′ ( x ) . S o m = 1 2 x = 1 2 . 64 = 5 8 . S o θ = a t a n ( 5 8 ) = 32.005 4 o . ⟹ θ 2 = 16.002 7 o . L i n e S P i s y = m ( x − . 64 ) + . 8. B u t f o r S , y = 0. S o l v i n g 0 = 5 8 ∗ ( x − . 64 ) + . 8 , x = − . 64 , a n d S ( − . 64 , 0 ) . ∴ S P = { . 64 − ( − . 64 ) } 2 + . 8 2 . ∠ S P O = 9 0 o T a n g e n t s S P a n d S N , f o r m s a k i t e w i t h r a d i i O P a n d O N ∴ I n Δ P S O , R = O P = S P ∗ t a n ( θ 2 ) = . 4329 P=(.64,.8).~~~ ~~Let ~tangent~from~P~meet~x-axis~at~S.\\ Let~f(x)=\sqrt x~~~~.~~Slope~m~of~SP,~say~tan\theta=f '(x).\\ So~m=\dfrac 1 {2\sqrt x}=\dfrac 1 {2 \sqrt{ .64}}=\dfrac 5 8.\\ So~\theta=atan \Big ( \dfrac 5 8 \Big )=32.0054^o.\\ \implies~\color{#3D99F6}{\dfrac \theta 2=16.0027^o.} \\ Line~SP~is~y=m(x-.64)+.8.~~~ But~for~S, ~y=0.~~~~\\ Solving~0=\dfrac 5 8*(x-.64)+.8, ~x=-.64,~and~S(-.64,0).\\ \therefore~SP=\sqrt{\{.64-(-.64)\}^2+.8^2}.~~~\angle~SPO=90^o \\ Tangents~SP~and~SN,~forms~a~kite~with~radii~OP~and~ON\\ \therefore In~\Delta~PSO,~~~R=OP=SP*tan \Big (\dfrac \theta 2 \Big)=.4329

Niranjan Khanderia - 3 years, 4 months ago
Guiseppi Butel
Oct 5, 2014

soln soln Here is my solution. The numerical quantities are identical to those given by Pranjal Jain, however my approach is clearer to me.

PO = R = ON = LM

PL = R cos P

PM = PL + LM = R cos P + R which equals 0.8

R(cos P + 1) = 0.8

R = 0.8/ cos P + 1

R = 0.4329

10000 * R = 4329

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...