Find the radius

Geometry Level 3

Let A B C D ABCD be a quadrilateral in which A B AB is parallel to C D CD and perpendicular to A D AD , B A = 3 C D BA = 3CD and the area of the quadrilateral is 4 square units. If a circle can be drawn touching all sides if the quadrilateral, then its radius is:

[3^(1/2)]/2 4 2[3^(1/2)] 2

Swastik Sahoo by Swastik Sahoo , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Marta Reece
Jun 14, 2017

From △ O C E \triangle OCE we can get tan ⁡ θ = R 3 a − R \tan\theta=\dfrac{R}{3a-R}

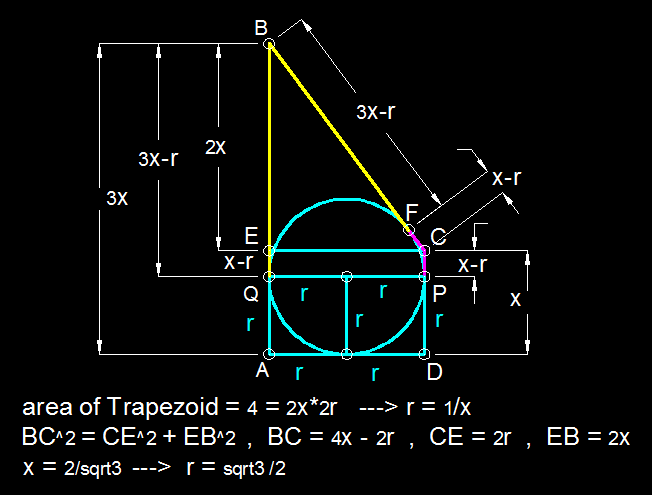
From △ B F C \triangle BFC likewise tan ⁡ 2 θ = 2 R 2 a = R a \tan2\theta=\dfrac{2R}{2a}=\dfrac Ra

The formula for a tangent of a double angle is tan ⁡ 2 θ = 2 tan ⁡ θ 1 − tan ⁡ 2 θ \tan2\theta=\dfrac{2\tan\theta}{1-\tan^2\theta}

Substituting into it R a = 2 × R 3 a − R 1 − ( R 3 a − R ) 2 \dfrac Ra=\dfrac{2\times\dfrac{R}{3a-R}}{1-\left(\dfrac{R}{3a-R}\right)^2}

This simplifies to a = 4 R 3 a=\dfrac{4R}{3}

Are of A B C D ABCD is [ A B C D ] = 2 R × a + 3 a 2 = 4 a R = 4 [ABCD]=2R\times \dfrac{a+3a}{2}=4aR=4

From that we get another relationship between a a and R R , namely a = 1 R a=\dfrac 1R

Combining the two, we get R = 3 4 R=\boxed{\dfrac{\sqrt3}{4}}

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Ahmad Saad
Nov 30, 2016

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...