Find the radius and the height
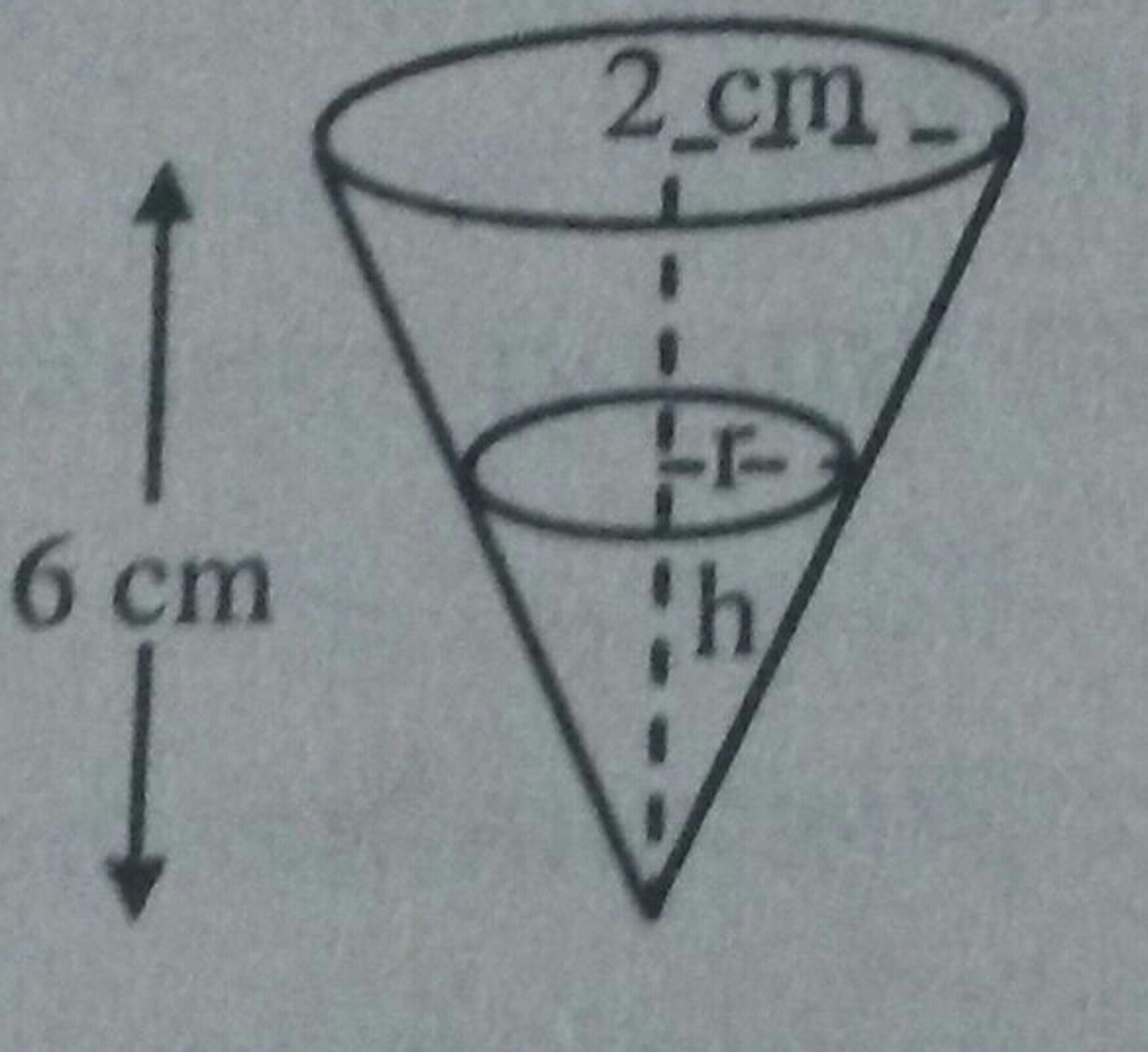
For a cone, radius is 2cm and height is 6cm.
When the cone is filled with water to half its volume, then find its radius and height.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
h : r = 6 : 2
Therefore, h = 3 r .
Also, the smaller cone is half the volume of the larger one, 2 3 = 2 r 3
Therefore, r = 3 4
Doesn't really validate the answer. It only validates that it is a possible solution because of the fact h:r = 3:1
Formula for the volume of a cone is V = 3 1 π r 2 h .
V c o n e = 3 1 π ( 2 2 ) ( 6 ) = 8 π ; V w a t e r = 2 1 ( 8 π ) = 4 π
By ratio and proportion in the diagram, we have: h r = 6 2 ⟹ r = 3 1 h
Now we substitute,
4 π = 3 1 π ( 3 1 h ) 2 ( h )
h 3 = 1 0 8
h = \leftroot − 1 \uproot 2 3 1 0 8 = 3 \leftroot − 1 \uproot 2 3 4
It follows that, r = 3 1 × 3 \leftroot − 1 \uproot 2 3 4 = \leftroot − 1 \uproot 2 3 4 . So h = 3 r .