Find the radius of the circle
 Hexagon
A
B
C
D
E
F
is inscribed in circle
O
, with
A
B
=
B
C
=
C
D
=
8
and
D
E
=
E
F
=
F
A
=
4
. Find the radius of the circle. If your answer can be expressed as
3
a
where
a
is square free, give your answer as
a
.
Hexagon
A
B
C
D
E
F
is inscribed in circle
O
, with
A
B
=
B
C
=
C
D
=
8
and
D
E
=
E
F
=
F
A
=
4
. Find the radius of the circle. If your answer can be expressed as
3
a
where
a
is square free, give your answer as
a
.
The answer is 112.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
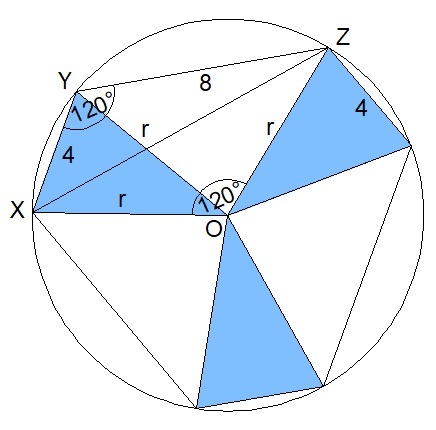 One way of solving this problem is rearranging the six triangles in a more symmetrical way. Denote the center of the circle by
O
, with
X
Y
=
4
and
Y
Z
=
8
adjacent sides of the rearranged hexagon. Notice that quadrilateral
X
O
Z
R
is exactly one-third of the entire hexagon. Therefore
∠
X
O
Z
=
3
3
6
0
=
1
2
0
. By the symmetry of the rearranged hexagon, all of its interior angles are equal, so
∠
X
Y
Z
=
6
7
2
0
=
1
2
0
.
One way of solving this problem is rearranging the six triangles in a more symmetrical way. Denote the center of the circle by
O
, with
X
Y
=
4
and
Y
Z
=
8
adjacent sides of the rearranged hexagon. Notice that quadrilateral
X
O
Z
R
is exactly one-third of the entire hexagon. Therefore
∠
X
O
Z
=
3
3
6
0
=
1
2
0
. By the symmetry of the rearranged hexagon, all of its interior angles are equal, so
∠
X
Y
Z
=
6
7
2
0
=
1
2
0
.
Let X Z = a , by law of cosines in △ X Z O , we have
a 2 = r 2 + r 2 − 2 r 2 cos 1 2 0 = 2 r 2 − 2 r 2 ( 2 − 1 ) = 3 r 2
by law of cosines in △ X Z Y , we have
a 2 = 4 2 + 8 2 − 2 ( 4 ) ( 8 ) cos 1 2 0 = 8 0 − 6 4 ( 2 − 1 ) = 1 1 2
a 2 = a 2
3 r 2 = 1 1 2
r = 3 1 1 2
Finally, the desired answer is 1 1 2 .
1 1 2 = 2 4 ⋅ 7 is not square-free.
How do you know YZ=8?, you didn't proved/showed this in your solution, it's the same as saying EA=8
Log in to reply
Y Z = 8 is the longer side of the rearranged hexagon. It is equal to the longer side of the original hexagon. Note that the six triangles were just reaarranged in a more symmetrical way for easy problem solving.
I too found sqrt(112/3) as the solution, that is why I looked at the solution to find out what I did wrong. A little disappointing that the conditions are not adapted!
I got a solution of sqrt(112/3), and brilliant says "correct" when I gave 112 as my answer. However, I maintain that this is wrong, because the problem stipulates that a must be square free; But 112 is divisible by 4, and is therefore not square free. Therefore, I claim there is no answer to this problem which satisfies the requested conditions. Ed Gray