Find the radius of the circle!
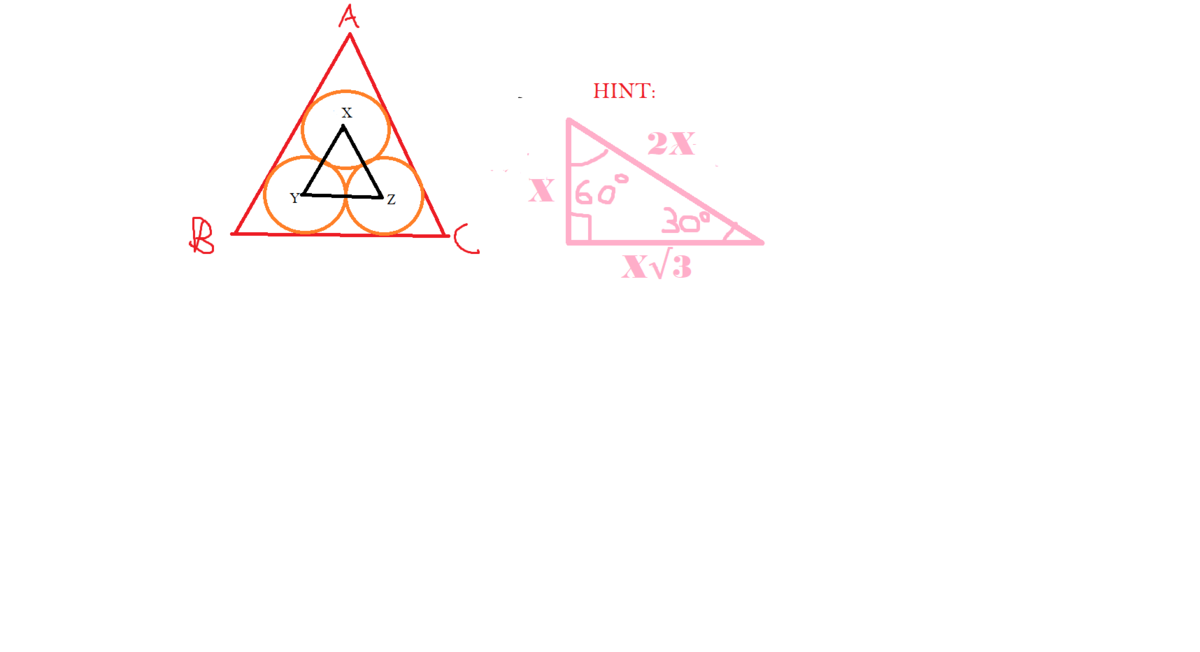
Three points A,B,C when connected together forms an Equilateral Triangle with Perimeter 36 Three *Identical * Circles were drawn inside the Triangle.
X,Y,Z are the center of the circles. When X,Y,Z are connected another Equilateral Triangle is formed. Can you find the radius of the circle?
The answer is 2.20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
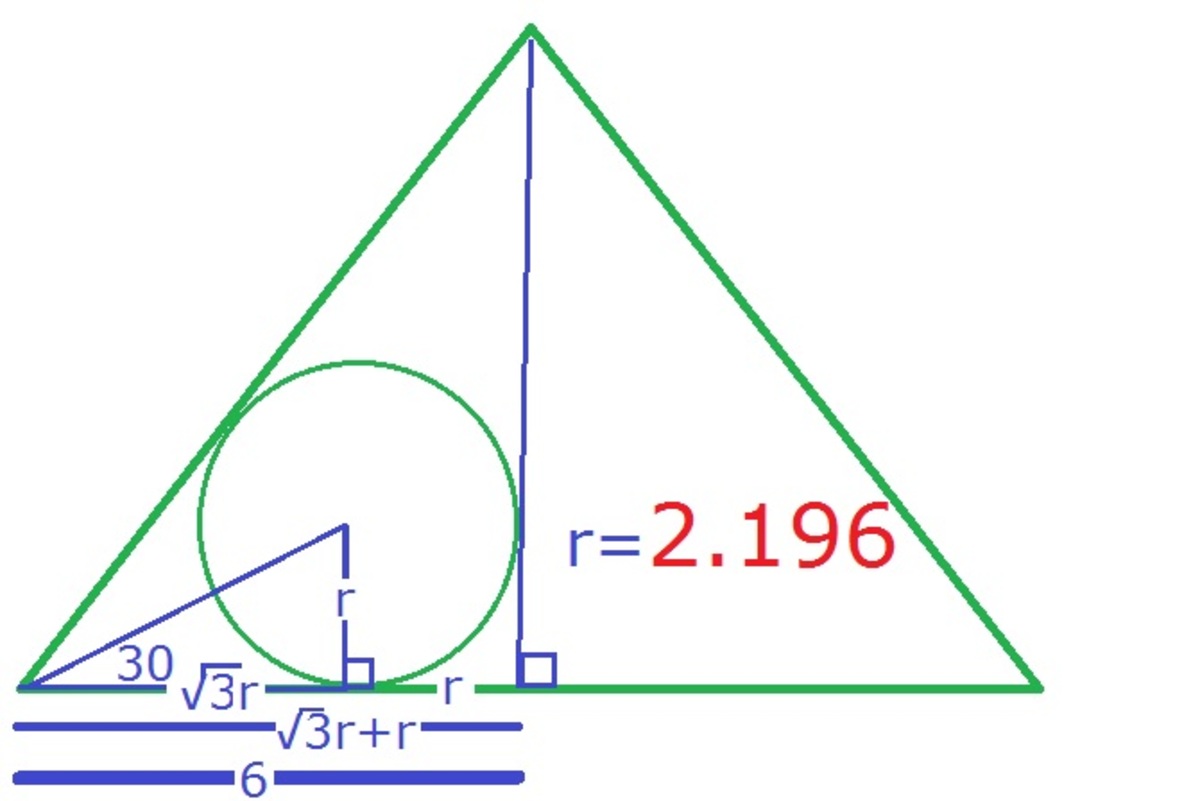
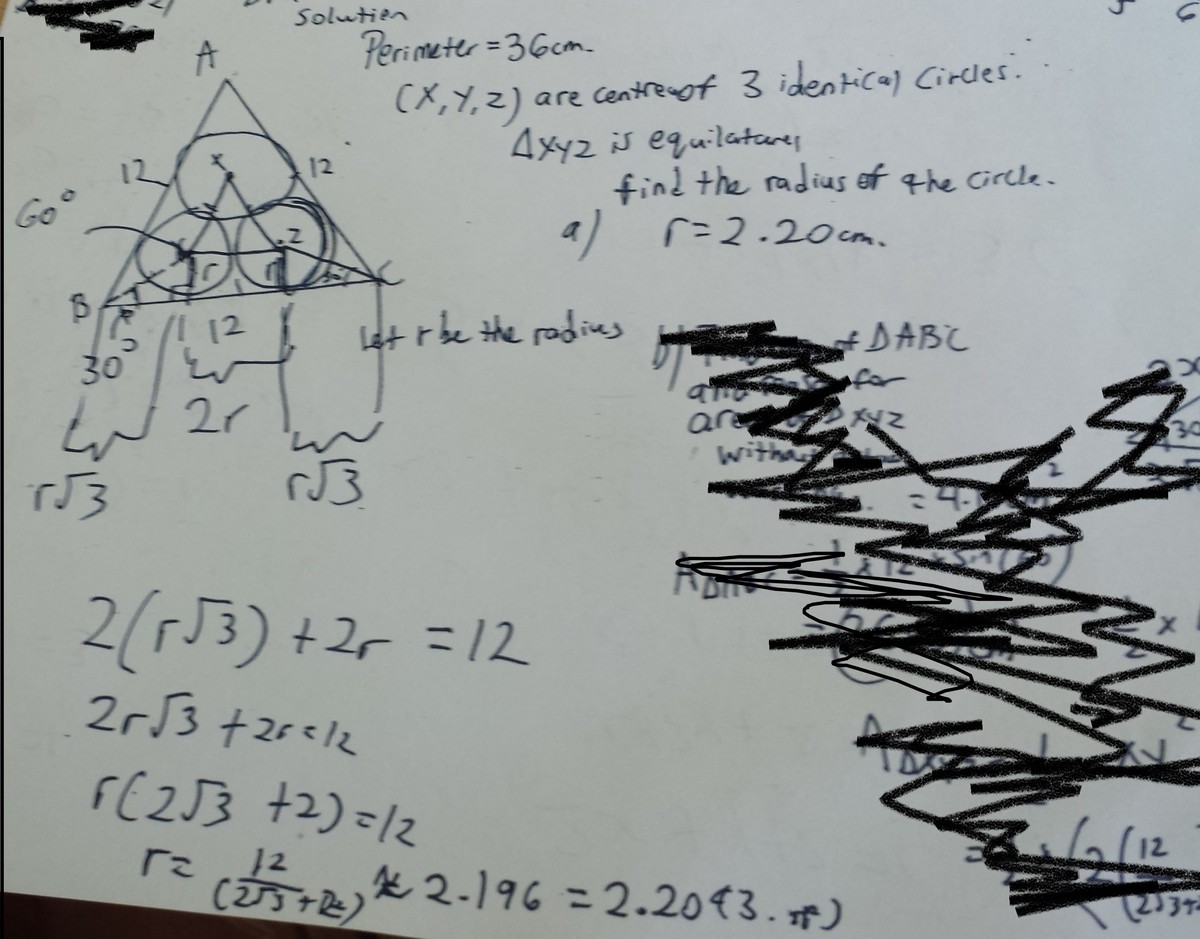
The shift method follows from the previous problem of mine. The proof is left for the readers to work out.
Let r denote the radius of the circle. Since all 3 inscribed circles have the same radius, we can shift equilateral triangle X Y Z as shown below.
Since in the original diagram the small triangle Δ X Y Z is positioned at the center of the large one, the altitude of B Y Z C is 3 r (from point O to the bottom). Then, since the length of Δ X Y Z is 2 r , then ∣ X O ∣ = 3 r , so the altitude of Δ A B C is 3 r + 3 r . Therefore, the radius of the circle is radius of circle r ( 3 + 3 ) r = altitude of Δ A B C = 6 3 = 3 + 3 6 3